L'histogramme
Objectif
REprésenter / Analyser / Partager
Durée
30 min
Coup de coeur
Mon outil favori
Ce que vous allez apprendre sur cette page
- Comprendre à quoi sert un histogramme
- Les étapes de construction de d'un histogramme
- Découvrir des exemples d'histogramme
Qu'est-ce qu'un histogramme ?
L'histogramme est un outil pour résumer graphiquement et rapidement des données collectées à partir d'un processus.
Il est possible d'obtenir ces données à partir de feuilles de relevés .
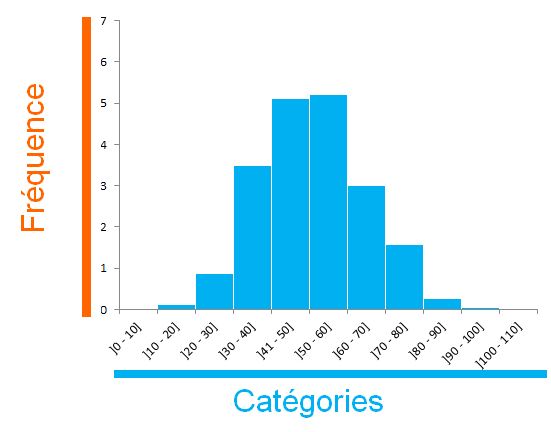
Sur l'axe verticale,on représente la fréquence ( nombre d'occurrences ) sous forme de barres de différentes hauteurs.
Sur l'axe des horizontale, on représente les catégories(ou groupes), qui peuvent être des valeurs, ou des classes (intervalles) de valeurs.
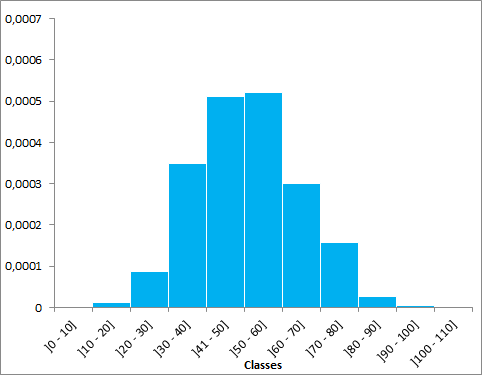
L'histogramme montre la forme des données, le centrage du processus, la variation et une distribution approximative des données.
Pourquoi utiliser un histogramme ?
L'histogramme permet d'avoir une première approche d'avoir des indications de la capabilité du processus. Pour cela, il faut comparer le centre et largeur de la distribution avec les limites de spécification.
L'histogramme est utile pour comparer une situation avant l'arrivée d'une amélioration et après l'amélioration. Ce type de comparaison est facile à réaliser.
Les étapes de construction d'un histogramme
Voici les étapes de construction d'un histogramme:
- Identifier le paramètre de processus à analyser ( Nombre de défaut sur un composant )
- Collectez les données avec la précision nécessaire
- Déterminer le nombre de classes nécessaires ( voir encadré ci-dessous)
- Dénombrer le nombre d'occurence pour chacune des classes
- Dessinez un histogramme basé sur la fréquence des données tombant à chaque intervalle.
Exemple d'histogramme
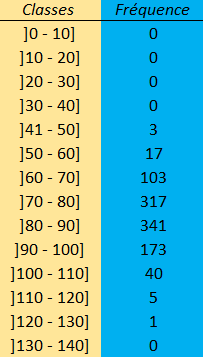
Le poids de 1000 individus est recueilli et donne le jeu de données suivant ci-dessous.
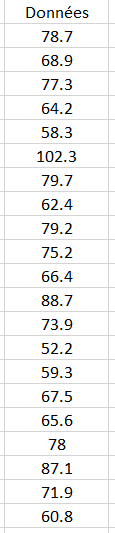
Vous avez ici un extrait des 21 premières valeurs. On remarquera tout de suite qu'il s'agit de variables continues. Or la construction d'un histogramme nécessite d'obtenir des valeur discrètes. Nous devons donc convertir les valeur continue en valeur discrètes. pour cela nous utilison des intervalles de valeurs.
Construction du tableau permettant la réalisation de l'histogramme
Construction du graphique
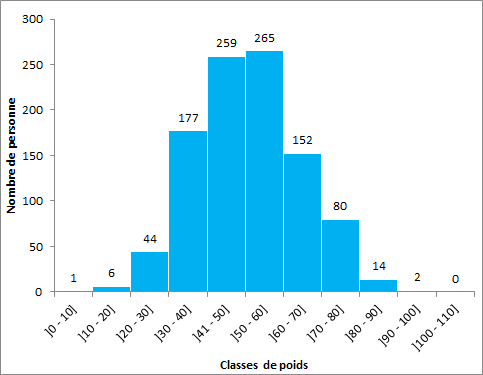
Choix du nombre de classe pour construire l'histogramme
L’histogramme est utile pour avoir une représentation visuelle des données. En faisant varier le nombre de classe nous modifions cette représentation visuelle. Il s'agit alors de trouver le nombre de classe qui facilitera l’interprétation des données.
Il n'y a pas une seule bonne réponse. Le choix du nombre de classe dépend de la nature de la distribution et du volume de données.
Le calcul du nombre de classe le plus simple que propose la littérature est le suivant K = √(N).
Les autres calculs possibles sont ceux de Rule ou de Sturge.
Autres informations concernant l'Histogramme ( Pour les curieux )
Les particularités de l'histogramme
Le graphique de type histogramme, se présente sous cette forme :
- Chaque surface de chaque barre a une surface proportionnelle à l'effectif.
- Les barres sont de largeur identiques
- La surface totale représente 100% des valeurs
- En ordonnée, on trouve soit les effectifs,
- En abscisse, on trouve les classes
Quel apparence a un histogramme ?
- Si les données sont des variables quantitatives discrètes, les barres sont disjointes.
- Si les données sont des variables quantitatives continues, les barres sont contiguës
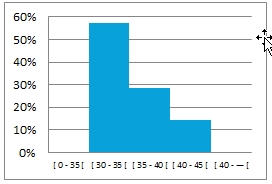
Le regroupement en classe d'une variable continue engendre une perte d'information. Pour pallier à cela, il est possible de diminuer l'amplitude des classes et donc, donc d'augmenter leur nombre.
La représentation ci-dessous indique une amplitude de classe de a=10.
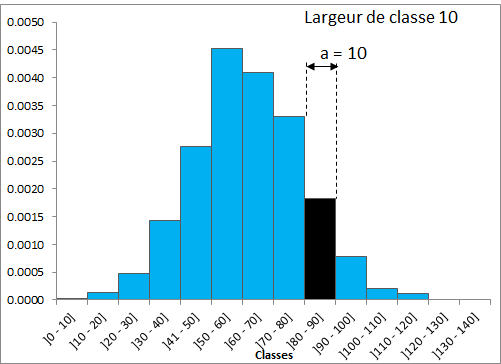
Cela se traduit par une diminution de la hauteur et de la largeur des barres. En revanche la somme des fréquences relative dans l'air total de l'histogramme est toujours égal à 100 % .
Pour pallier ce problème, il faut diviser la probabilité p(x) par l'amplitude de la classe a soit la largeur du rectangle. f(x)=p(x)/a
L'air de chaque rectangle représente toujours la fréquence relative de la classe et F de X est appelée densité de fréquence relative.
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT
