Les tests statistiques ou test d'hypothéses
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
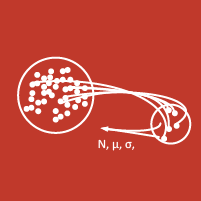 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
 Tests statistiques
Tests statistiques
Principes des tests statistiques de comparaison
Les tests statistiques permettent de réaliser des comparaisons et d'en tirer des conclusions.
Sur quoi sont réalisés tests statistiques ?
Les tests statistiques sont de manière générale réalisés sur plusieurs échantillons issus d'une population ou sur un échantillon et une population. Dans les deux cas l'objet du test et de comparer des populations. En effet, même si les calculs sont réalisés sur les paramètres des échantillons, la finalité est bien de tirer des conclusion sur les populations en elles-mêmes.
Le schéma ci-dessous montre le principe d'un test statistique de comparaison de moyenne.
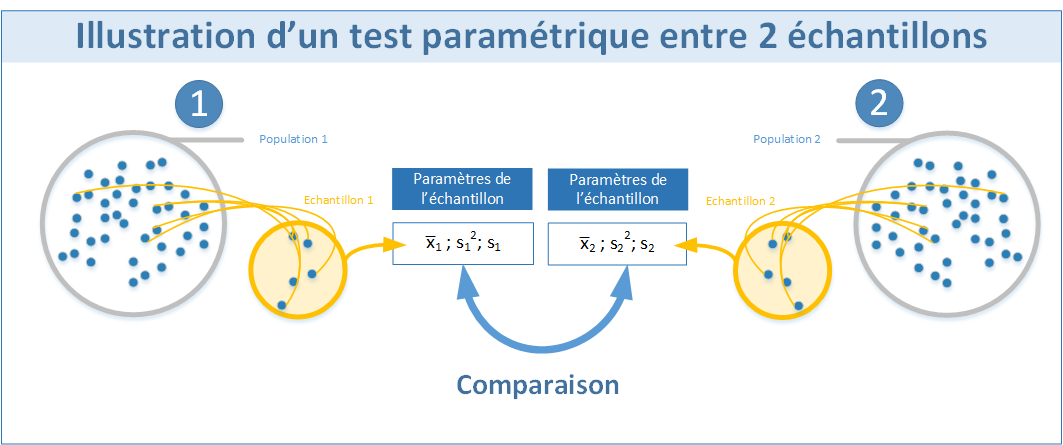
Qu'est-ce qui est comparé ?
La comparaison permet d'indiquer s'il y a une différence significative ou non entre des paramètres statistiques ou des distributions.
Comme nous l'avons vu dans le dossier sur les paramètres statistiques , les paramètres peuvent être par exemple une moyenne ou encore un écart-type ou d'autres éléments…. Il s'agit dans tous les cas d'un chiffre.
Les distributions peuvent suivre la loi normale, une loi de Student, une loi binomiale... Dans ce cas-là, c'est le mode de répartition de la variable qui fait l'objet de la comparaison.
Hasard ou réelle différence ?
Nous trouverons presque toujours des différences entre deux séries de données. Le but de ces tests et d'indiquer si la différence observée est due au hasard ou si cette différence est réelle. C'est-à-dire que les deux populations concernées ne sont pas semblables.
En réalisant des tests statistiques sur des échantillons et non sur la population nous devons admettre un risque d'erreur.
La formulation d'hypothèses
Les tests statistiques se basent sur des hypothèses.
Les hypothèses sont déterminées avant la réalisation du test afin de répondre à une question. Les tests statistiques doivent avoir pour objectif de vérifier si une hypothèse est justifiée ou non.
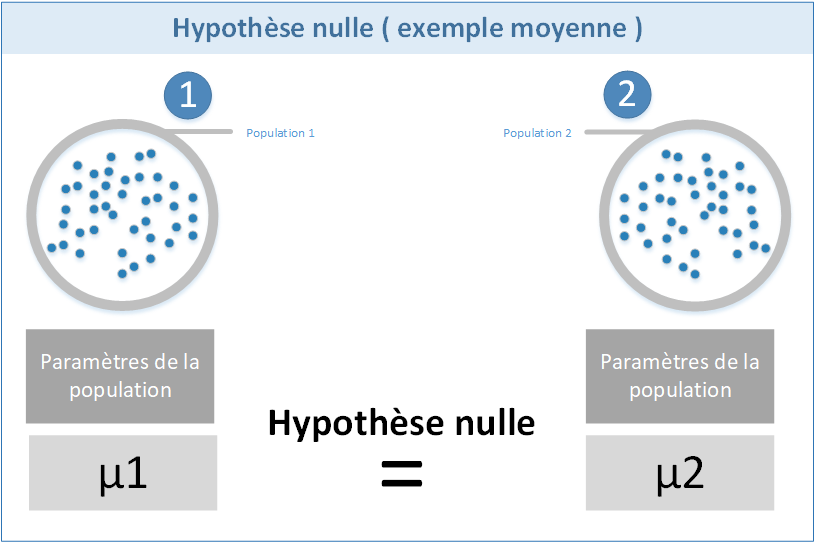
L'hypothèse nulle H0
La première hypothèse est l'hypothèse nulle H0 c'est-à-dire l'hypothèse qui consiste à dire que les paramètres ou les distributions entre les deux populations sont identiques. Formuler l'hypothèse nulle indique que l’on suppose que l'écart observé provient des fluctuations d'échantillonnage.
Hypothèse alternative H1
L'hypothèse alternative H1 est l'hypothèse qui est retenue au cas où l'hypothèse H0 et rejetée, c'est-à-dire que la différence observée est trop grande pour qu'on l’attribue à une simple fluctuation d'échantillonnage. On suppose donc que dans ce cas les paramètres ou les distributions de population sont différents.
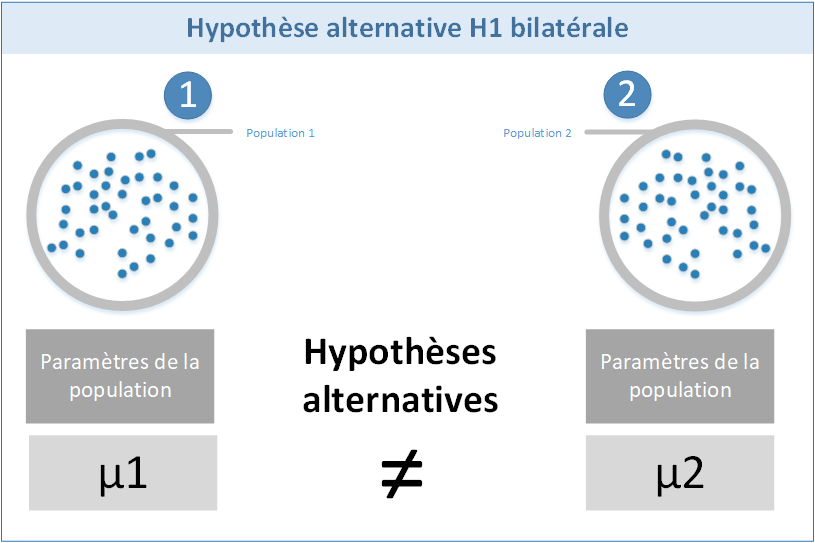
Hypothèse alternative H1 bilatérale
Cette hypothèse alternative H1 peut-être soit bilatérale ou unilatérale.
L'hypothèse H1 bilatérale est l’hypothèse formulée lorsque l'on ne cherche pas à connaître le sens de la différence entre les deux populations. On dit juste que les populations sont différentes.
Hypothèse alternative H1 unilatérale
L'hypothèse unilatérale H1 est l'hypothèse alternative qui est définie lorsque l'on souhaite connaître le sens de l'inégalité entre les paramètres des 2 populations.

L'hypothèse est soit acceptée ou rejetée à l'issue du test.
Conditions d'application des tests
Les conditions d'application des tests sont divers.
Condition 1: Adéquation entre la distribution étudiée et la distribution théorique
La première condition est l'adéquation entre la distribution étudiée et la distribution théorique sur laquelle est basée le test.
Condition 2: Comparabilité des échantillons
La seconde condition et la comparabilité des échantillons. Les échantillons doivent avoir des tailles comparables.
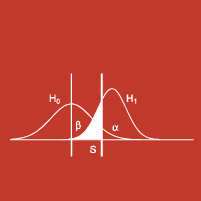
Le calcul des risques alpha α et bêta β
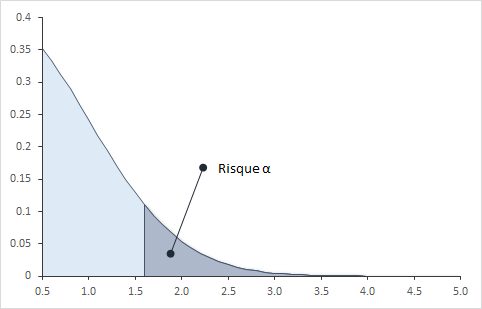
Le risque alpha α
En rejetant H0 on prend un risque que l'on appelle le risque alpha α . Il s'agit du risque de se tromper en rejetant H0 si dans la réalité H0 est vrai.
On appelle également ce risque le risque de première espèce.
Le risque alpha α est déterminé avant la réalisation du test.
il est commun de fixer ce risque d'erreur alpha à 5%. Bien sûr il est possible de changer ce risque en fonction du domaine dans lequel on applique le test.
Dans des domaines où les enjeux sécurité sont forts ce risque pourra par exemple être de 1% ou 0,1%.
En fixant ce risque nous devons trouver un équilibre entre fixer un risque trop faible et ne jamais rien conclure et fixer un risque trop élevé qui conduirait le décideur à se tromper fréquemment et à subir les éventuelles conséquences.
Le degré de signification p
Le risque alpha α est déterminé a priori, c'est-à-dire avant la réalisation du test. Le degré de signification p est une valeur qui est déterminée a posteriori c'est-à-dire après la réalisation des calculs. Le degré de signification p est la probabilité, si H0 est vraie, d'observer au moins une valeur aussi grande que celle qui était calculée par le test. Le risque est un risque de première espèce (Type 1).
En d'autres termes, le degré de signification indique la probabilité d'avoir rejeter H0 si on a fixé le risque alpha α égale à p au lieu de alpha.
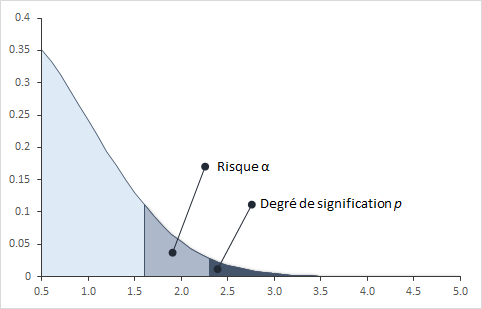
le risque bêta β
Le risque bêta est le risque de ne pas avoir rejeté H0 alors que H1 est vrai. Cela arrive lorsqu'il existe une différence entre les paramètres étudiés, mais que la valeur observée se situe néanmoins dans l'intervalle comprenant 95 % des valeurs probables. Ce risque est appelé risque de deuxième espèce. (Type 2)
La puissance d'un test se calcule de la manière suivante : 1 - β
La puissance d'un test est liée à la taille des effectifs des échantillons. Plus la taille des échantillons augmente plus la puissance augmente et plus le risque bêta diminue. La valeur du risque bêta n'intervient pas dans l'interprétation d'un test car on ne sait pas la calculer. Le risque bêta et uniquement utilisé pour le calcul de la taille des échantillons.
Voici une synthèse des risques

Les étapes de la réalisation des tests
Le calcul des tests de comparaison les étapes du calcul sont les suivantes :
- Réaliser le calcul de l'écart entre les paramètres
- Si le modèle théorique suit une loi Z normale centrée réduite ou une loi T de Student alors on fera la différence entre les deux valeurs.
- Si le modèle théorique suit une loi F de Fisher alors on réalise le rapport entre deux valeurs.
- Si le modèle théorique suit une loi du Chi2 alors on réalise la différence entre les pourcentages
- comparer la valeur obtenue avec le modèle de distribution théorique
- soit la valeur trouvée est probable, on en conclut que la différence observée entre les paramètres étudiés n'est pas significative.
La différence peut s'expliquer par les fluctuations d'échantillonnage, on rejette alors H0 - soit la valeur trouvée excède une valeur seuil qui la rend peu probable. Il est encore possible que ce résultat soit due à une simple fluctuation d'échantillonnage mais on décide de ne pas tenir compte de cette faible probabilité on rejette l'hypothèse nulle H0 et on accepte l'hypothèse H1 d'une différence réelle entre les paramètres. On dit alors qu'il y a une différence significative entre les paramètres.
- Interprétation des tests
- Soit on accepte l'hypothèse H0. On en conclut que rien ne permet d'affirmer qu'il y a une différence entre les paramètres.
Remarque: on affirme jamais qu'une hypothèse H0 nulle est vraie, car elle aurait pu être rejetée si la puissance du test avait été plus élevée. - Soit on rejette H0 si l'hypothèse H0 bilatérale avait été initialement sélectionnée on conclura que les paramètres étudiés sont différents si l'hypothèse H1 unilatéral avait été sélectionné, on conclura que l'un des paramètres est inférieur ou supérieur à l'autre.
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT
