
La distribution de poisson
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
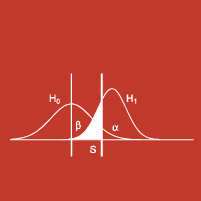 Tests statistiques
Tests statistiques
Qu'est-ce que la distribution de Poisson ?
La distribution de Poisson est une distribution de probabilité discrète.
La distribution de Poisson décrit la distribution de probabilités lorsque les événements étudiés ont lieu dans une fourchette de temps délimité ou dans un lieu défini.
La probabilité qu'un événement survienne est la même pour chaque unité de temps et d'espace.
Le nombre d'événements qui survient dans une unité de temps et d'espace est indépendant du nombre d'événements qui survient dans une autre unité.
Quand utiliser la loi de Poisson ?
Deux situations l'exigent
- Lorsque la loi binomiale ne peut pas s'appliquer en raison des limites de calcul des outils informatiques (nombre d'événements trop élevé)
- Lorsque le taille de l'échantillon n est inconnu.
| Cas d'utilisation de la loi de Poisson | Exemple |
|---|---|
| Variables discrètes | 1,2,3,4... |
| nombre d'occurrences d'un événement | Comptabilisation du nombre de fois que l'événement survient. |
| Espace ou temps défini. | Les lancés de pièces de monnaie sont réalisés dans des conditions identiques. |
Notation :
- x correspond au nombre d'occurrences observées
- μ correspond au nombre moyen d'occurrences dans l'intervalle de temps ou dans l'espace considéré.
- P(x) probabilité d'observer x occurrence de l'événement
- e est une constante, la base logarithmique naturels(=2.71828)
La formule est la suivante : 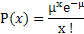
Exemple : Village
Exemple : Dans un village, un collégien assis sous le porche d'une maison compte le nombre de voitures qui passe devant lui en 10 minutes. Il sait, suite à de nombreuses observations, que le nombre de voitures est en moyenne de 25. Quelle est la probabilité que ce collégien compte demain un nombre 30 voitures ?
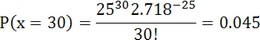
Note : Il est possible d'arriver à ce résultat sans passer par le calcul. En effet, il existe une table de poisson qui permet de trouver les résultats de façon rapide. Elle est disponible en page 4 en suivant le lien suivant : Table de la loi de poisson .
Dans un premier temps, il faut repérer la colonne correspondant à la valeur de μ, il faut ensuite trouver la ligne correspondant à la valeur de x.
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT

