
Paramètres statistiques : Moyenne, Médiane, Etendue, Ecart-type...
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
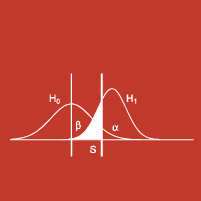 Tests statistiques
Tests statistiques
Ce qu'il faut retenir...
- Les paramètres statistiques permettent de résumer la distribution d'une variable quantitative
- Il y a 2 types de paramètres : position et dispersion
- paramètres de position
- Moyenne, médiane...
- paramètres de dispersion
- Écart-type...
- paramètres de position
Le fichier exemple
Télécharger le fichier exemple
Lien : parametretatistique.xlsx
Les paramètres
Raccourcis vers les sections de la page
- Nombre
- Somme
- Moyenne
- mediane
- Mode
- Étendue
- IQR
- Variance
- Ecartype
- Estimateur ecart type
- Estimateur ecart type calculé à partir de l'étendue
Les paramètres élémentaires
Comptabiliser le nombre de valeurs
La première question que l'on peut se poser lorsque l'on a un jeu de données à analyser est de déterminer le nombre de valeurs.

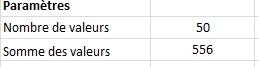
Somme de valeurs
Un autre paramètre utile est de connaître la somme de ces valeurs.
Valeurs extrêmes
Les valeurs extrêmes sont les valeurs minimum et maximum.

Les paramètres de position
Tendance centrale
Ces paramètres permettent de rendre de compte du point d'équilibre du jeu de donnée.
Moyenne
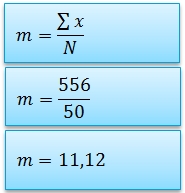
La moyenne se calcule en divisant la somme des valeurs par le nombre d'observations.

À retenir - Moyenne
- le résumé le plus connu des informations
Ses propriétés :
- La moyenne des écarts à la moyenne est nulle.
- Peu sensible aux fluctuations d'échantillonnage.
- Sensible aux valeurs extrêmes.
- Mauvais résumé si la distribution est très dissymétrique
Médiane
Pour trouver la médiane, il faut classer les valeurs du plus petit au plus grand.Il suffit de regarder ou se trouve le chiffre médian dans une distribution. Il y a autant de sujets inférieurs à la médiane que supérieurs à la médiane.
Il s'agit donc de la distribution qui la partage en deux parties égales.
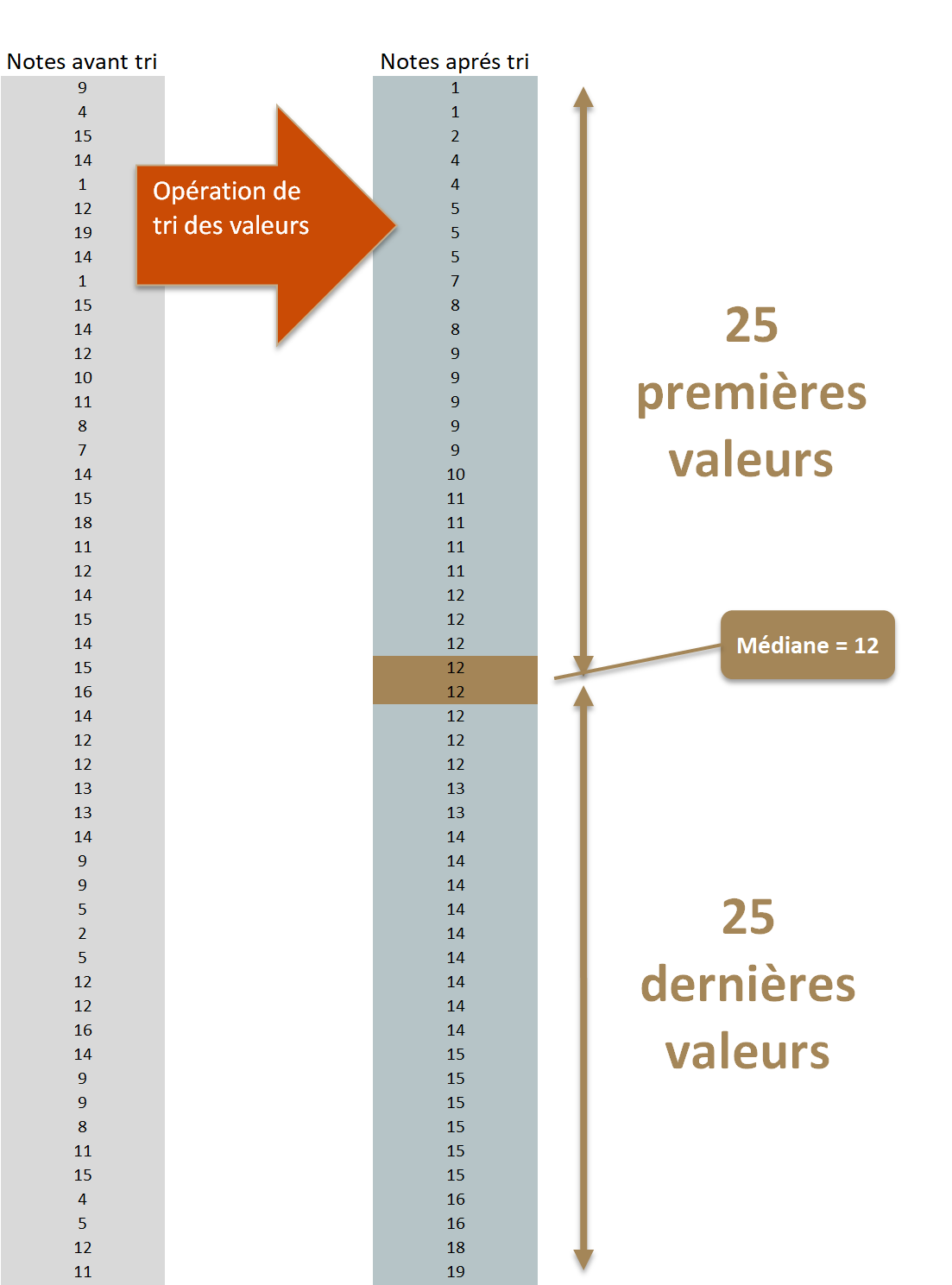
À retenir - médiane
Ses propriétés :
- La médiane est peu sensible aux valeurs extrêmes
- Ne se prête pas bien aux calculs mathématiques.
Mode
Il s'agit de la valeur la plus fréquemment retrouvé. Il s'agit de la valeur associée à la plus grande fréquence (absolue ou relative)
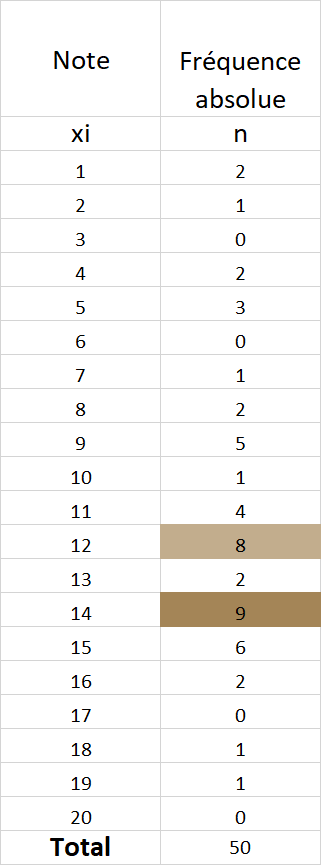
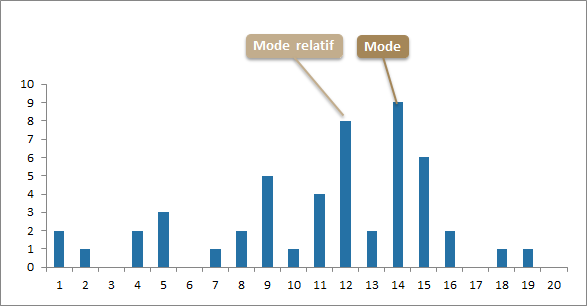
À retenir - Mode
Ses propriétés :
- Il est possible d'avoir plusieurs modes.
- Les modes relatifs sont toutes les valeurs précédées ou suivies de valeurs de fréquences inférieures.

Quantiles
Les quantiles divisent la distribution en plusieurs secteurs d'intérêt.
Quartiles
Les quantiles habituellement calculés sont les quartiles :
- Q1: 25% des valeurs sont inférieures au premier quartile
- Q2 ou médiane: 50% des valeurs sont inférieures au deuxième quartile
- Q3 : 75% des valeurs sont inférieures au troisième quartile
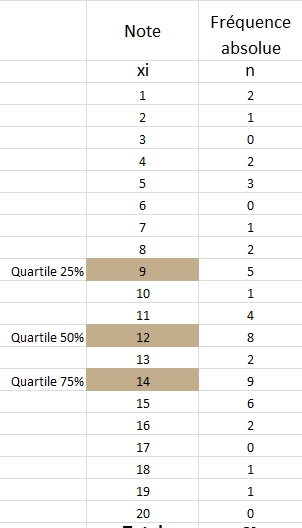
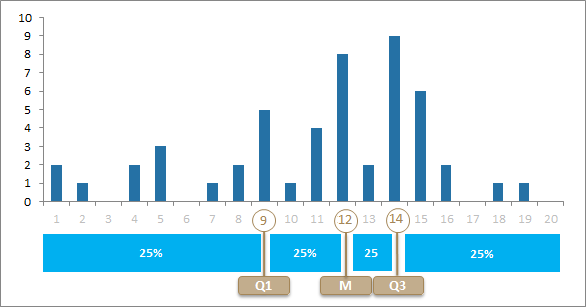
On interprète le graphique de façon suivante :
- 25% des valeurs sont inférieures ou égale à 9
- 50% des valeurs sont inférieures ou égale à 12
- 75% des valeurs sont inférieures ou égale à 14
Il est possible de choisir d'autre quantiles tel que Déciles, les Centiles, ou des Percentiles particuliers (par exemple 5% ou 95%).
À retenir - Quantiles
Ses propriétés :
- Il est possible de couper la distribution en
- Quartiles
- Déciles
- Centiles
- Percentiles particuliers
Les paramètres de dispersion
Ces paramètres rendent compte de l'étalement des données. Cela permet de montrer si les données sont éloignées ou proches de la moyenne.
Étendue
Il s'agit de différence entre les valeurs extrêmes de la distribution.

À retenir - Etendue
Ses propriétés :
- Le plus facile à calculer
- Très sensible aux valeurs extrêmes
- Indépendant de la valeur de position
- Ne tient pas compte des valeurs comprises entre les valeurs minimum et maximum
Intervalle Interquartile IQR
Il s'agit de la différence entre les valeurs du troisième et premier quartile.

IQR = 14 - 9 = 5
À retenir - IQR
Ses propriétés :
- Peu sensible aux valeurs extrêmes
- Indépendant de la valeur de position
Écarts à la moyenne
Il s'agit des écarts de chaque valeur par rapport à la moyenne.
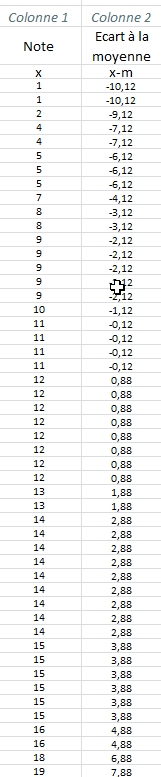
À retenir - Ecart à la moyenne
- On constate des écarts positifs et des écarts négatifs.
- L'addition de tous ces écarts donne comme résultat une valeur égale. Cela ne permet pas de donner d'information sur la dispersion.
- Il s'agit des valeurs absolues des écarts à la moyenne
L'écart absolu moyen
Il s'agit de la moyenne arithmétique des valeurs absolues des écarts de chaque valeur par rapport à la moyenne.
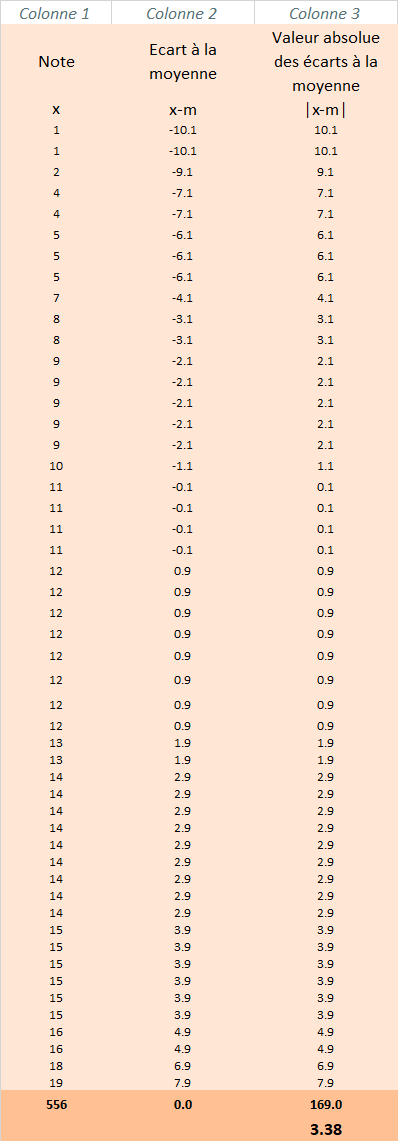
Sur cette dernière ligne, vous visualisez la moyenne calculée à partir des valeurs de cette même colonne.
À retenir - Ecart moyen absolu
- Prend en compte toutes les observations et montre la dispersion des données autour de la moyenne.
- Peu sensible aux valeurs extrêmes
- Relativement simple à calculer et comprendre.
- Il ne permet pas la réalisation de calculs ultérieurs car les signes algébriques sont ignorés.
Variance
Il s'agit de la moyenne des carrés des écarts.
Il rend compte de l'éloignement de chaque valeur par rapport à la moyenne.

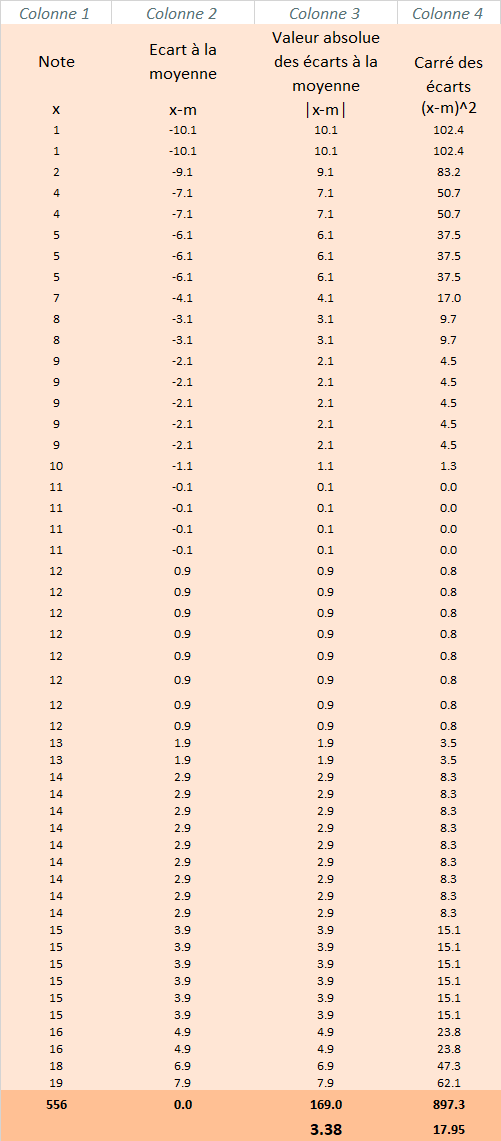
À retenir - Variance
Ses propriétés :
- Toujours positif
- Dépendant de la valeur de position
- Pas d'unité du même ordre que la valeur étudié
Écart-type
Il s'agit de la racine carré de la variance

Écart-type établi à partir d'un échantillon
Si on prend une série de n observations indépendante xi dont la moyenne est x .
Soit par l'écart-type expérimental

Remarque : généralement, le symbole σ est employé pour désigner l'écart-type, et s l'estimateur de l'écart-type. Ainsi, lorsque l'on calcule l'écart-type d'une grandeur à partir d'un échantillon, seule une estimation s de l'écart-type σ peut être obtenue. Le calcul est lui aussi différent puisque l'on utilise un nombre de degrés de liberté de n-1, car on ne connait pas l'ensemble de la population.
Soit par l'étendue
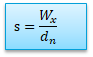
Ws (noté parfois R) est l'étendue et dn est un coefficient dont la valeur dépend de la taille de l'échantillon.
Si l'on veut calculer l'écart-type avec cette méthode, on doit supposer que la distribution des valeurs de la population suit une loi normale. Elle est lue dans le tableau suivant :
La valeur de dn sera récupérée dans le tableau suivant :
| n | d2 |
|---|---|
| 2 | 1.128 |
| 3 | 1.693 |
| 4 | 2.059 |
| 5 | 2.326 |
| 6 | 2.534 |
| 7 | 2.704 |
| 8 | 2.847 |
| 9 | 2.970 |
| 10 | 3.078 |
| 11 | 3.173 |
| 12 | 3.258 |
| 13 | 3.336 |
| 14 | 3.407 |
| 15 | 3.472 |
| 16 | 3.532 |
| 17 | 3.588 |
| 18 | 3.640 |
| 19 | 3.689 |
| 20 | 3.735 |
| 21 | 3.778 |
| 22 | 3.819 |
| 23 | 3.858 |
| 24 | 3.895 |
| 25 | 3.931 |
Si la taille de l'échantillon est supérieur à 10, le meilleur estimateur de σ est l'écart-type expérimental.
À retenir - écart type
Ses propriétés :
- Mesure la dispersion autour de la moyenne
- Toujours positif
- De même unité que la moyenne
- Il donne une idée de la distribution
- Sensible aux valeurs extrêmes
Si la distribution suit une loi normale, il est possible de dire que :
- entre le 0 et ±1σ vous aurez 68.3% de vos observations.
- entre le 0 et ±2σ vous aurez 95.4% de vos observations.
- entre le 0 et ±3σ vous aurez 99.7.% de vos observations.
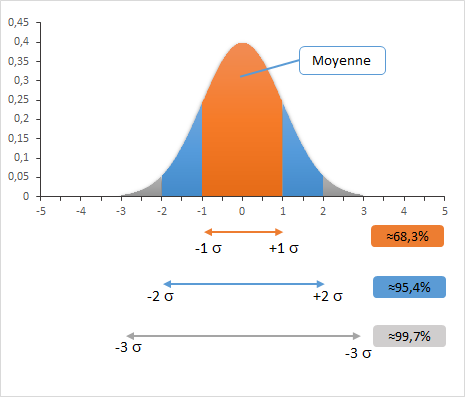
Vous trouverez un dossier complet sur ce sujet sur la page distribution normale .
Combinaison position/dispersion
Le coefficient de variation
Il combine les paramètres de moyenne et d'écart-type.
Il permet de comparer 2 variables de nature différente.

Détection de valeurs aberrantes
Règle de J.tuckey
Une valeur aberrante est une donnée qui s'écarte de façon marquée de l'ensemble des autres données. Une règle pratiques utilisées pour identifier une valeur aberrante est la suivante :
Règle : Une donnée peut-être appeler valeur aberrante si elle s'écarte d'une distance d'au moins 1,5x au-dessus du troisième quartile ou en dessous du premier quartier.
Une valeur aberrante doit être examinée avec soin pour identifier la cause d'éventuelles de cet écart important par rapport à l'ensemble des données.
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT

