
L'échantillonnage
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
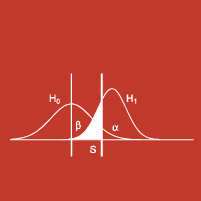 Tests statistiques
Tests statistiques
Population et échantillon
Une population : L'ensemble des unités considérés par le statisticien. Il peut s'agir par exemple de l'ensemble des élèves d'une école.
Note : Lorsque l'on parle de population, on ne parle pas nécessairement d'êtres humain. Par exemple, on pourra considérer comme population, l'ensemble des habitantes de Tunis ou encore les pommes du pommier en bas de chez moi.
Un échantillon : Sous-ensemble de la population choisi pour l'étude. Un échantillon est par nature incomplet, mais peu s'avérer tout à fait suffisant pour atteindre les objectifs de l'étude avec un niveau de confiance suffisant.
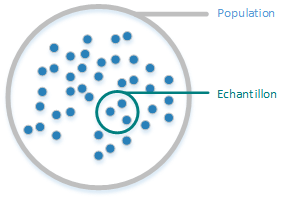
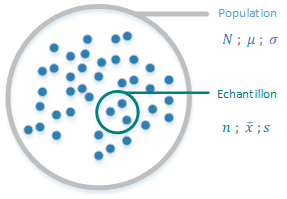
Les mesures relatives à une population sont les paramètres.
Les mesures relatives à un échantillon sont appelées statistiques (ou estimateurs).
Nous allons voir que les terminologies et les symboles sont différents entre une population et un échantillon.
Les symboles
| Correspondance | Population | Echantillon |
|---|---|---|
| Moyenne | μ |
x
|
| Variance | α2 |
s2 |
| Ecart-type | α |
s |
| Taille | N |
n |
| Pourcentage | π |
p |
Pourquoi faire de l'échantillonnage ?
Lorsque l'on souhaite avoir des informations sur une population, il n'est pas toujours possible de considérer l'ensemble des entités.
Si par exemple votre population est l'ensemble des élèves d'une école, il est possible d'observer toute la population concernée. (recensement)
Si votre population est le nombre d'habitants du Maroc, alors là, il est plus difficile de faire des observations sur l'ensemble des individus, dans ce cas-là, on peut prélever des échantillons représentatifs de la population. L'image obtenue doit être fidèle à la population. L'avantage de l'échantillonnage et d'économiser des ressources.
L'échantillon doit fournir suffisamment d'information pour qu'une inférence soit possible à propos des caractéristiques de la population ait le niveau de prévision requis. En effet, une estimation de paramètres (Moyenne ou écart type) d'une population à partir d'un échantillon s'accompagne nécessairement d'un degré de confiance.
Les avantages de l'échantillonnage sont :
- un coût moins élevé qu'un recensement
- une prise de décision plus rapide
- des destructions de produits limités (cas des contrôles destructifs).
- la précision des échantillonnages peut être très proche de celle d'un recensement.
Les enjeux de l'échantillonnage
Or, les résultats des échantillons ne donnent jamais exactement les mêmes valeurs que les caractéristiques de la population. On appelle cela l'erreur d'échantillonnage ou biais d'échantillonnage.
Heureusement, l'erreur d'échantillonnage est quantifiable et les résultats obtenus à partir des échantillons sont utilisables pour la prise de décision.
En effet, associé à un certain degré de confiance, il sera possible de faire des approximations de la population.
Le choix de l'échantillon
On appelle sondage la méthode utilisée pour échantillonner.
L'enjeu du choix de l'échantillon est de déterminer de quelles unités doivent être prises en compte pour constituer un échantillon représentatif de la population.
Les échantillonnages probabilistes
Un échantillon probabiliste est un échantillon pour lequel les chances de prélever chaque élément est connu avant même le prélèvement de l'échantillon. On notera les techniques d'échantillonnage suivantes :
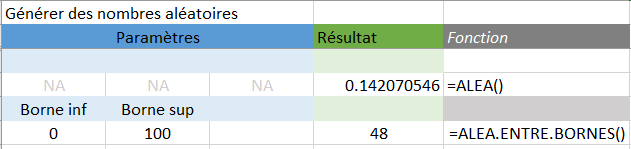
- l'échantillonnage aléatoire simple : La probabilité de sélection de chaque membre d'une population a une chance égale d'être inclus à l'intérieur de l'échantillon. On peut, au besoin, utiliser la fonction aléatoire d'un tableur pour faire ce choix. (ALEA.ENTRE.BORNES ou ALEA) .
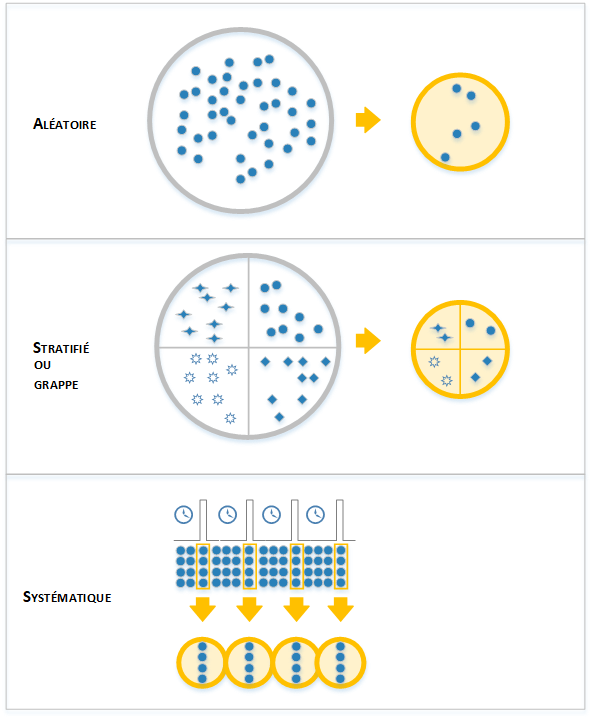
- Échantillonnage stratifié: Il s'agit de diviser la popopluation en strates (regroupement par catégorie) distinctes en fonction de l'importance relative de chaque catégorie les résultats sont pondérés. (Les bananes de groupe 1 représente 55% des bananes vendu en France, Le groupe 2 représente 17%, le groupe 3...) Le prélèvement effectué sur les bananes de groupe 1 sera d'avantage pondéré que celui du groupe 2.
- l'échantillonnage en grappes ; la population est, là encore, subdivisée en groupe. Par exemple, prenons le cas d'un contrôle qualité d'un lot de 1000 pièces organisé en plateaux de 20 pièces. Au lieu de prélever 2 pièces dans chacun des 5 plateaux, le qualiticien pourra prélever l'ensemble des pièces dans les plateaux n°10,n°13 n°27,n°30 ,n°43 ; soit un total de 100 pièces.
- L'échantillonnage systématique: L'expérimentateur détermine un écart, ou un intervalle, systématique entre chaque unité sélectionnée. Par exemple, toutes les 25 pièces. Par exemple, nous avons un listing de 5000 noms avec l'âge de ces personnes, nous souhaitons un échantillon de 250 personnes, on prélèvera alors le 20ème nom, puis le 40ème nom, puis le 60ème nom etc...
Les échantillonnages non-probabilistes
Les échantillons non-probabilistes est un échantillon dans lequel le jugement de l'expérimentateur, ou d'autres facteurs affecte le résultat de l'échantillon.
On trouvera parmi ces méthodes :
- Les échantillons discrétionnaires. Ce sont des échantillons pour lesquels l'expérimentateur estime qu'ils sont représentatifs de la population. Il est toutefois difficile d'estimer à quel point cette estimation est proche de la réalité. En effet, la pertinence des résultats dépend de l'expérience de l'expérimentateur.
- L'échantillon issu d'une participation volontaire est une autre méthode qui dépend de la volonté des personnes sondés, cela engendre un biais dépendant de l'intérêt des personnes sondés sur le sujet.
- L'échantillon de commodité est également issu d'un échantillonnage non-probabiliste qui dépend par exemple de l'endroit d'où est réalisé le sondage. Par exemple, devant un restaurant. On parle de commodité car l'échantillon sera en partie déterminé par la disponibilité des individus. Ce type d'échantillonnage pose la question de la représentativité des résultats.
Détermination de la taille d'échantillonnage
La formule donnant la taille minimale de l'échantillon est :
Rappel des notations
- n est la taille de la population
- t coefficient de marge traduit du tableau de confiance
- p Proportion de la population qui représente une caractéristique donnée. (Si p est inconnu, on utilise p=0.5)
- e est la marge d'erreur choisie pour l'estimation (par exemple, si e=0.01, alors cela signifie que l'on veut connaître la proportion réelle à 1% près).
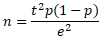
Mise en œuvre des échnatillonnages
Nous vous invitons à consulter des exemples concrets d'échantillonnage sur la page contrôle qualité .
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT

