CommentProgresser.com
Le théorème central limite - estimation d'une moyenne
Statistiques descriptives
La statistique - Enjeux
Démarche statistique
Les variables
Les tableaux
Les graphiques
Parametres statistiques
Distributions statistique
Probabilite
Distribution statistiques
Distribution normale
Distribution binomiale
Distribution de Poisson
Courbe de Gauss avec Excel
Echantillonnage
Estimation de paramètres
Théorème central limite
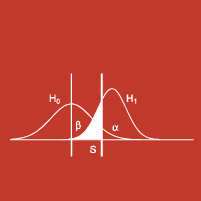Tests statistiques
Pourquoi le théorème central limite est important ?
Le théorème central limite est sans doute le théorème le plus important des statistiques. C'est le théorème qui nous est le plus utile pour les expérimentations que nous faisons dans le monde. Il est utilisé pour les démarches inférentielles.
Alors n'ayez pas peur de ce nom abstrait, et lancez vous dans la découverte de ses secrets.
Les fondements du théorème central limite
La distribution d'échantillonnage des moyennes
Comment construire la distribution d'échantillonnage des moyennes ?
Pour comprendre le théorème, je vous propose de découvrir le mécanisme de construction d'échantillonnage en 6 étapes.
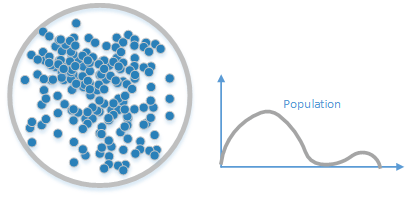
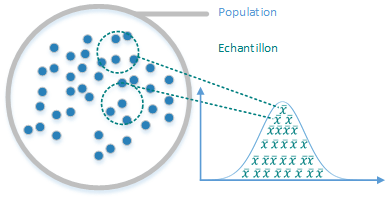
Etape 1 : Prenons comme exemple la population suivante pour laquelle nous pouvons visualiser la distribution. On notera que la distribution ne suit aucune loi. Elle est totalement aléatoire.
Sur la gauche, vous trouverez l'ensemble des individus.
Sur la droite, vous trouverez sa distribution totalement aléatoire.
Etape 2 : Prélevons 5 échantillons
Note : La taille de l'échantillon est de 15 éléments.
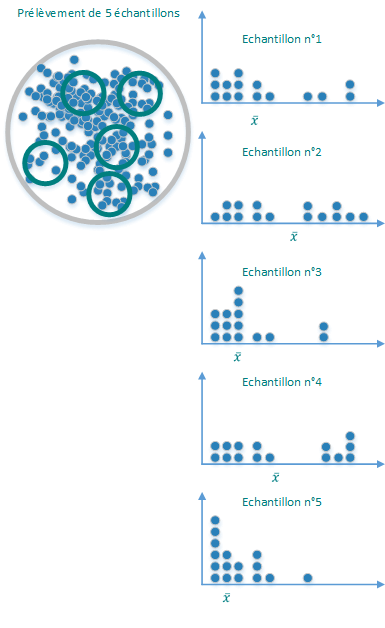
Etape 3 : On calcul les moyennes et on les positionne sur un graphique
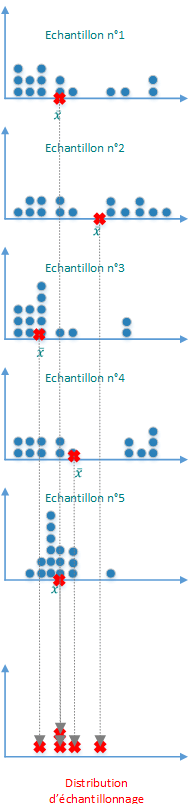
On peut maintenant visualiser les prémices d'une distribution d'échantillonnage avec ces 5 premiers échantillons.
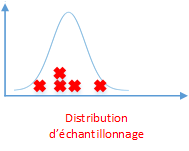
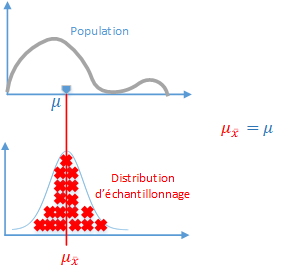
Imaginons que vous ayez prélevé un grand nombre échantillons voici à quoi ressemblerait la distribution.
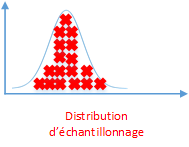
On remarque que les moyennes des échantillons ont tendance à se rapprocher de la moyenne de la population car les valeurs extrêmes s'équilibrent. La moyenne d'échantillon est une approximation de la moyenne de la population. En effet, la plupart des valeurs sont proches de la moyenne de la population, tout en ne correspondant jamais exactement à celle-ci. Toutefois, on remarque qu'il existe un lien entre a moyenne d'échantillon et la moyenne de la population.
En conséquence, on peut affirmer que la moyenne de la distribution d'échantillonnage correspond à la moyenne de la population.
Ce que dit le théorème central limite ?
1.A) Si la taille de l'échantillon est suffisamment grand (>30) alors la distribution d'échantillonnage se rapproche de la distribution de la loi normale.
1.B) Si la distribution de la population est distribuée selon la loi normale, la distribution d'échantillonnage suit une loi normale indépendamment de la taille de l'échantillon.
2) La moyenne de la distribution d'échantillonnage des moyennes des échantillons est égale à la moyenne de la distribution de la population originale.
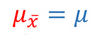
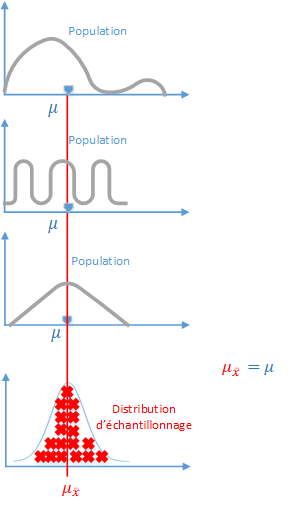
Cela est vrai quelle que soit la forme de la distribution originale.
Voici quelques exemples.
3) l'écart-type de la moyenne m est égale à l'écart-type des valeurs de l'échantillon population divisée par la racine carrée de la taille d'échantillon.
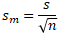
Remarques
Il ne faut pas confondre l'écart-type s des valeurs de l'échantillon est-ce avec l'écart-type de la moyenne Sm.
De plus, cette formule ne s'applique que si la taille de l'échantillon est négligeable par rapport à la taille de la population, c'est-à-dire n < 10 % de la taille de la population.
Avec cette formule, on peut faire les constats suivants : Plus le σ de la population diminue plus le σ X diminue. Egalement plus n augmente plus σ X diminue.
Détermination de l'intervalle de confiance d'une moyenne
Le théorème central limite va nous aider pour estimer la valeur de la moyenne inconnue d'une population à partir d'une observation d'un seul échantillon. Ils nous faut donc estimer l'intervalle dans lequel la moyenne inconnue à la plus grande probabilité de se trouver.
On sait (voir dossier
loi normale
) qu'il y a 95 % de chance que la moyenne μ de la population se trouve compris dans l'intervalle m-1.96 et +1.96.
On appel cet intervalle de confiance, Intervalle de confiance à 95 %
Distribution d'échantillonnage de pourcentage
La distribution d'échantillonnage de pourcentage est une distribution des pourcentages de tous les échantillons possibles qui peuvent être pris dans une situation donnée, ou les échantillons sont des échantillons simples d'un nombre fixe n.
Rappel des notations
- π est le pourcentage de population.
- N est la taille de la population
- X est le nombre d'individu
- μp est la moyenne de la distribution d'échantillonnage des pourcentages
- p est le pourcentage de l'échantillon
- σp est l'écart-type de la distribution d'échantillonnage des pourcentages
Moyenne de la distribution d'échantillonnage des pourcentages
Calcul de la moyenne de la population
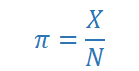
La moyenne de distribution d'échantillonnage est égale à la moyenne de la population.
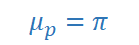
Écart-type de la distribution d'échantillonnage des pourcentages
L'erreur type du pourcentage est égale à l'écart-type de la distribution d'échantillonnage des pourcentages et est représenté par : σp
La formule est la suivante :
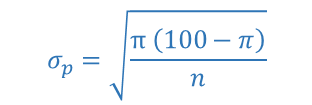
Par exemple, si on prend la longueur des mots d'un livre, on sait que ces longueurs ne suivent pas une loi normale, par contre si on prend comme échantillon une page du livre, et que l'on fait la même chose pour toutes les pages du livre on verra que les moyennes suivront une loi normale.
Pour aller plus loin consulter également le site qui constitue une importante source de connaissance : http://onlinestatbook.com/
Titre : Statistique descriptive et inférentielle avec Excel: Approche par l'exemple
Auteur : Argentine Vidal
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT
