
La distribution binomiale
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
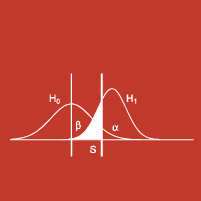 Tests statistiques
Tests statistiques
Avant d'aborder la loi binomiale, il est important de comprendre ce qu'est la loi de Bernoulli.
I) La loi de Bernoulli
Dénombrement d'un variable qualitative binaire
Une bonne manière de résumer une variable binaire consiste à procéder à un dénombrement.
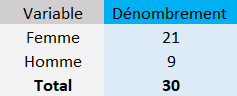
Transformation d'une variable binaire en une variable de Bernoulli
Pour résumer une variable binaire, on peut également procéder à une transformation. Il s'agit alors de transformer la variable binaire en une variable quantitative dont les modalités possibles sont 1 et 0.
On choisira arbitrairement quelle valeur correspond à 1 et quelle valeur correspond à 0.
Dans notre exemple, on choisira.
- Femme = 1
- Homme = 0
Calcul des paramètres
Cette transformation permet alors de calculer les paramètres statistiques suivants :
Moyenne
La moyenne est égale à la somme des modalités codées 1 divisé par le nombre de valeur N.
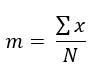
Elle est donc égale à la proportion P de la modalité codée 1.
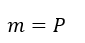
Dans notre exemple, :
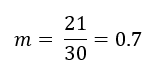
Variance
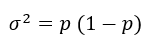
La variance d'une variable de Bernoulli a une propirété particulière puisque que, au maximum, elle peut atteindre 0.25.
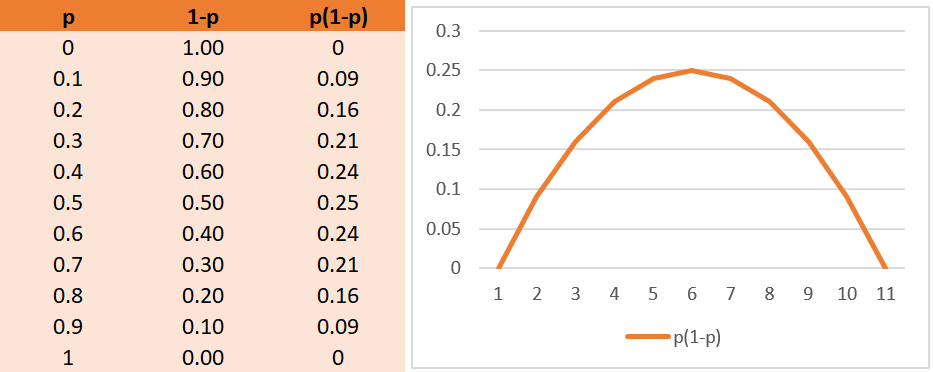
Dans notre exemple, elle est égale à :
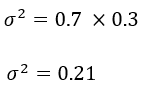
Ecart-type
l'écart-type est, bien évidemment, égal à la racine carrée de la variance.
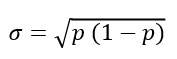
Epreuve de Bernoulli
Une épreuve de Bernoulli est une expérience aléatoire dont l'issue se traduit soit par un "succès" soit par un "échec".
Notation:
- p est la probabilité de succès à un essai
- q est la probabilité d'échec à un essai. q = (1 - p)
Exemple avec Pile ou Face

Avec 2 jets
Si on jette 2 fois la pièce, 4 situations sont possibles.
Chacune de ces situations a 25% de chance de se produire.

Quelle est la probabilité de tirer une seule fois pile ?
Elle est présente dans la situation 1 et dans la situation 2. Il faut donc faire la somme de ces 2 situations soit une probabilité de 5%.
Quelle est la probabilité de tirer deux fois pile ?
Elle est présente dans la situation 4 uniquement, la probabilité est donc de 0.25.
Avec 3 jets
Si on jette 3 fois la pièce, 4 situations sont possibles.
Chacune de ces situations a 25% de chance de se produire.

Quelle est la probabilité que le résultat du premier jet soit pile et que le second soit face ?
Elle est présente uniquement dans la situation 1. La probabilité est de 25%.
Quelle est la probabilité de tirer une seule fois pile ?
Elle est présente dans la situation 1 et dans la situation 2. Il faut donc faire la somme de ces 2 situations soit une probabilité de 50%.
Quelle est la probabilité de tirer deux fois pile ?
Elle est présente dans la situation 4 uniquement, la probabilité est donc de 25%.
3 jets avec un même probabilité pour pile ou face
Voici un exemple avec 3 jets :
Chacune de ces situations à une probabilité de 0.125 de survenir.
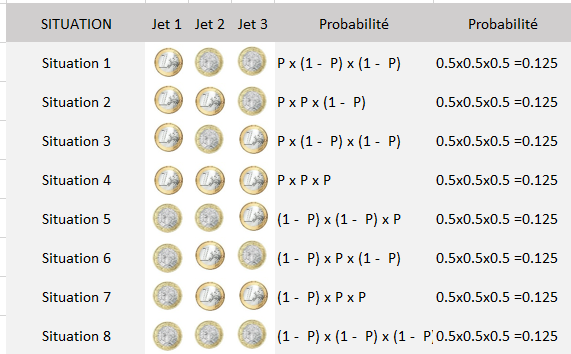
Lorsque nous prenons l'exemple d'une pièce de monnaie non truquée la probabilité respective de chaque côté de la pièce est de 0.5. En conséquence, les probabilités de chaque situation sont les mêmes.
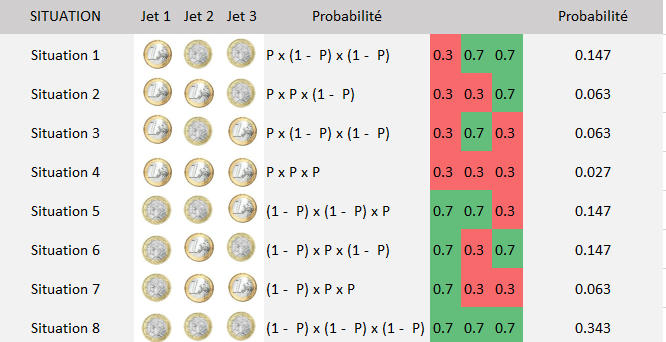
3 jets avec un probabilité différente de trouver pile ou face
Si nous prenons par exemple une pièce truquée dont la probabilité de tomber sur pile n'est que de 0.3 alors les probabilités de chaque situation seront changées.
Avec cette pièce truquée, la probabilité de tomber 3 fois sur pile n'est que de 2.7%.
Généralisation
La probabilité de trouver 1 fois pile pour n lancés peut se généraliser avec la formule suivante :
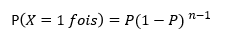
La probabilité de trouver k fois pile pour n lancés peut se généraliser avec la formule suivante : 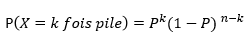
Cette probabilité ne correspond qu'à une situation donnée. (Par exemple la situation 1). Pour connaître la probabilité de toutes les situations possibles, il faut calculer le nombre de combinaisons dans laquelle ce cas de figure arrive. (Voir chapitre combinaison ci-desssous)
Combinaison
Notation :
- n correspond au nombre d'objets de l'ensemble
- r correspond au nombre d'objets du sous-ensemble choisi parmi les n objets.
Une combinaison est une sélection de r élément parmi un jeu de n objets distincts (sans prise en compte de l'ordre) parmi lesquels les r éléments sont sélectionnés. Le symbole nCr est utilisé pour désigner le nombre de possibilités de choisir r élément parmi n.
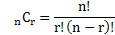
- n! représente le produit de tous les entier de n à 1
- r! représente le produit de tous les entier de r à 1
Rappel le symbole"!" signifie factoriel et se calcule comme suit : n!=n*(n-1)(n-2)...
Imaginons que nous ayons 4 jetons de quatre couleurs différentes : Vert, bleu, jaune et rouge. On demande à une personne de piocher à l'aveugle deux jetons.
Combien de combinaisons (de couples) possibles la personne pourra t'elle tirer ?
Interprétation de l'énoncé : Il y a 4 jetons dans l'ensemble donc n sera égale à 4.
L'individu sélectionne 2 jetons parmi 4 donc r sera égale à 2. On cherche le nombre de combinaisons possibles qui sera calculé avec la formule ci-dessous.
Le résultat de notre exemple donne :
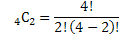
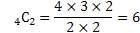
Il y a donc 6 combinaisons possibles.
II) La distribution binomiale
La distribution binomiale décrit la distribution de probabilités lorsqu'il y a 2 résultats possibles à chaque essai. (appelé succès ou échec)
Le résultat d'un essai doit être indépendant des résultats des autres essais.
La loi binomiale s'applique donc quand il y a un nombre défini de répétitions d'une même expérience dans les mêmes conditions.
La probabilité de succès est constante à chaque tirage.
Cas d'utilisation de la loi binomiale
| Cas | Exemple |
|---|---|
| Variables discrètes | 1,2,3,4... |
| Deux résultats possibles | Nombre "pair "ou"impair"; "coté pile" ou "coté face" ; produit "bon" ou "défectueux" |
| Essais répétitifs et dans les mêmes conditions | Les lancés de pièces de monnaie dans des conditions identiques. |
| Essais indépendants | Le résultat du premier lancé de pièces n'a pas d'incidence sur le second lancé. |
La notion de combinaison doit être présentée avant d'aborder l'utilisation des probabilités binomiales.
Calcul de la probabilité binomiale avec une formule
La formule de calcul du nombre de combinaisons est utilisée par la formule de la loi binomiale.
Le succès est le résultat pour lequel nous souhaitons déterminer la distribution de probabilité. Pour calculer la probabilité d'obtenir r succès en n essai il faut utiliser la formule suivante :
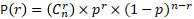
Notation :
- n correspond au nombre d'objet de l'ensemble
- r correspond au nombre d'objet du sous-ensemble choisi parmi les n objets
- p est la probabilité de succès à un essai
- q est la probabilité d'échec à un essai.
- P(r) est la probabilité d'obtenir r succès
Lors du même essai la somme de la probabilité de succès p et de la probabilité d'échec q est égale à 1 : p+k=1
Dans le service de contrôle d'entrée, un qualiticien souhaite savoir quel risque il prend lors du contrôle des pièces d'un fournisseur "laqualitécameconnait". Le qualiticien sait par expérience que ce fournisseur lui fournit 5% de pièces non-conformes et livre des lots d'une quantité de 400 pièces.
Le contrôle qualité effectue habituellement un contrôle par échantillonnage de 8 pièces sur les 400 pièces livrées.
Quel est le risque que sur les 8 pièces prélevés qu'un défaut soit détecté alors que le lot présente 5% de pièces non-conformes ?
Interprétation de l'énoncé :
- n=8
- r=1
- p=0.05
- q=95
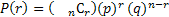
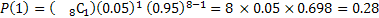
Il a donc 28% de chance de tomber sur 1 défaut.
Ce qui intéressera le qualiticien est la probabilité de détecter un défaut ou plus dans l'échantillon. Pour ce faire, nous devons additionner les probabilités de détecter 1, 2, 3...8 défauts.
| Résultats | Note de l'examen |
|---|---|
| P(r=0) | 66,34% |
| P(r=1) | 28% |
| P(r=2) | 5,15% |
| P(r=3) | 0,54% |
| P(r=4) | 0,04% |
| P(r=5) | 0% |
| P(r=6) | 0% |
| P(r=7) | 0% |
| P(r=8) | 0% |
| Total | 100% |
Avec ce type d'échantillonnage le contrôle d'entrée ne détectera de pièces non-conformes que dans 33% des cas.
27,93% 5,15% 0,54% 0,04%= 33%
Il y a donc seulement 33% de chances de détecter des non-conformités avec cette taille de prélèvement.
Note : Il est possible d'arriver à ce résultat sans passer par le calcul. En effet, il existe une table binomiale qui permet de trouver les résultats de façon rapide. Elle est disponible sur le lien suivant : Table de la loi binomiale .
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT

