Le contrôle par échantillonnage
Qu'est-ce que le contrôle par échantillonnage ?
Le contrôle un échantillonnage est aussi appelé contrôle par prélèvement. Le principe de ce contrôle et de tirer des conclusions sur la conformité dans lot à partir des résultats obtenus sur un échantillon. Ce type de contrôle diminue les inconvénients du contrôle à 100%. Il réduit les frais de contrôle et est la seule alternative au contrôle à 100 %
Plan d'échantillonnage simple
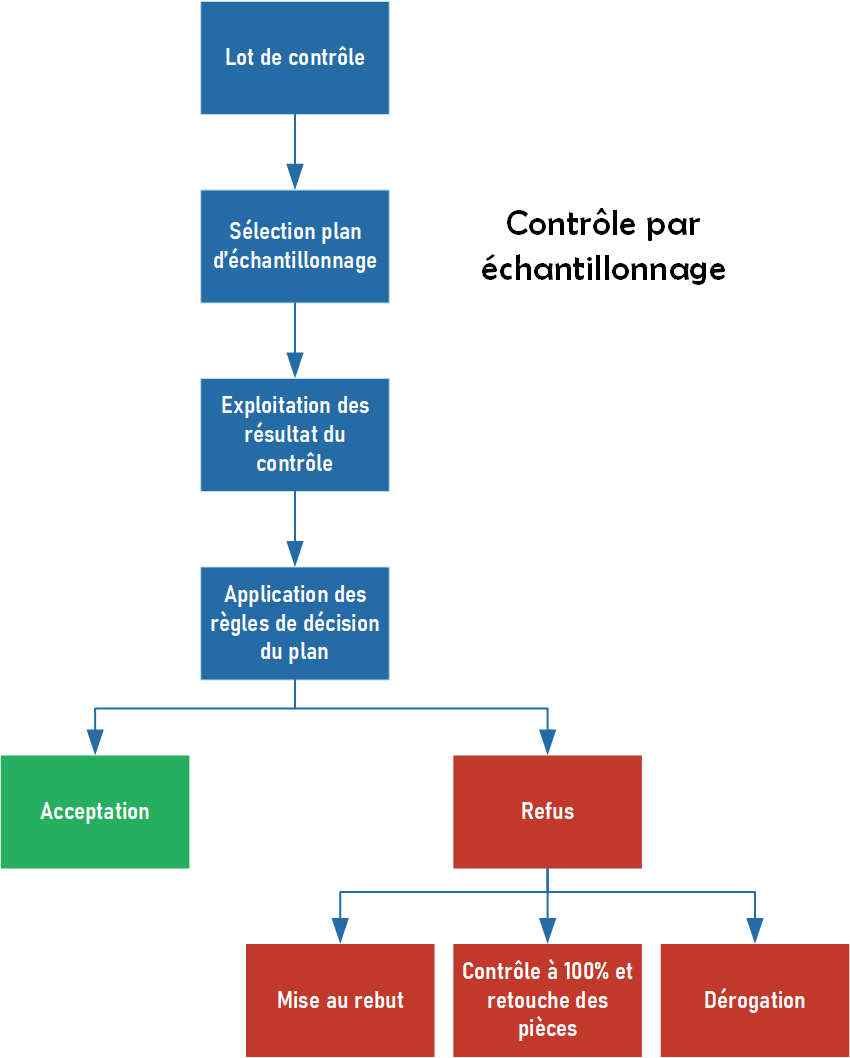
Processus de contrôle par échantillonnage
Exemples de contrôle par échantillonnage
Exemple 1 : Exemple d'application de la loi binomiale pour un contrôle industriel
L'entreprise “Précijuste” fabrique des axes en acier qui sont décolletés par une machine CNC. Ces pièces doivent respecter un cahier des charges esthétique très rigoureux. L'état de surface est contrôlé visuellement. D'après l'expérience du département de contrôle qualité, la machine-outil produit environ 6% de pièces défectueuses pour cause esthétique.
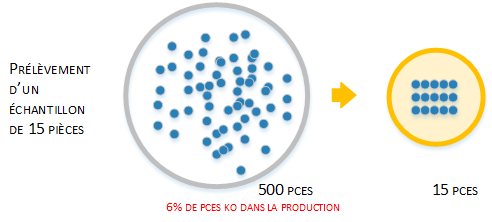
Un lot de 500 pièces vient d'être fabriqué. On prélève au hasard 15 pièces de ce lot.
Pour bien comprendre ce qu'est l'échantillonnage, on peut schématiser la situation avec une représentation comme ci-dessous :
Question n°1 : Dans un échantillon de cette taille, combien de pièces défectueuses peut-on s'attendre à observer en moyenne ?
Notations
- n correspond au nombre de produits prélevés
- p est la proportion de produits non-conformes obtenus naturellement par le processus de production.
Dans notre exemple, le résultat sera :
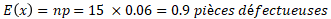
Question n°2 : Quelle est la probabilité d'observer dans un échantillon de taille n=15, 2 pièces dont l'état de surface serait non-conforme ?
La situation peut se schématiser comme suit :
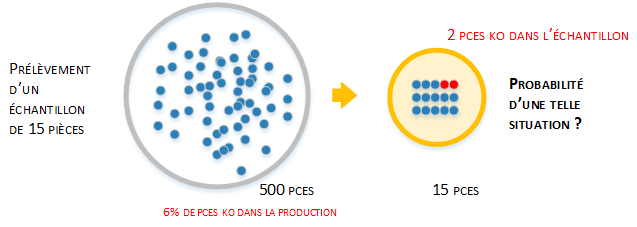
Notation :
- n correspond au nombre de produits prélevés
- r correspond au nombre de produits dont on cherche la probabilité d'apparition parmi les n objets
- p est la proportion de produits non-conformes obtenus naturellement par le processus de production.
- P(r) est la probabilité d'obtenir r produits défectueux dans l'échantillon
Une fois les notations posées, reprenons les éléments de l'énoncé. Le problème peut être décortiqué en trois parties.
La premiere partie identifie les informations dont nous avons besoin pour les calculs, La deuxième partie présente le calcul en lui-même
La dernière partie présente la réponse qui est recherchée à la question.
Ci-dessous, vous trouverez le mécanisme de raisonnement.

Il s'agit là d'une décomposition qu'il est intéressant de réaliser pour vos premières mises en situation. Bien évidemment une fois que cela vous sera familier vous pourrez aller beaucoup plus rapidement au résultat.
Le calcul se résume simplement par :
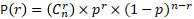
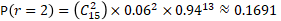
Pour en savoir plus sur l'utilisation de la loi binomiale consulter le dossier sur la loi binomiale .
Application avec Excel :
Saisissez les paramètres tels qu'indiqué dans les cellules en bleu.
- Utiliser la formule LOI.BINOMIALE.N().
- Renseigner les paramètres dans la formule.
- Terminer avec le paramètre "FAUX"
- Appuyez sur entrée


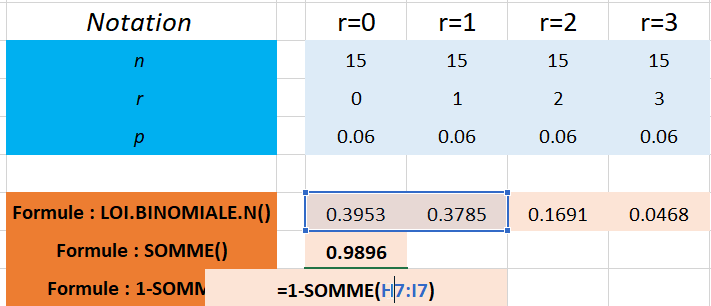
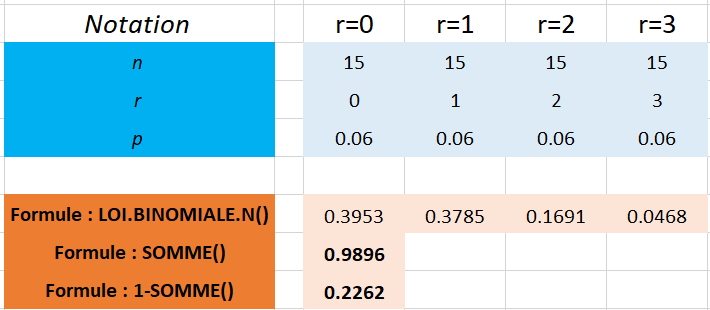
Question n°3 : Quelle est la probabilité d'observer au plus 3 pièces défectueuses dans un échantillon de taille n = 15 ?
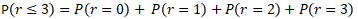
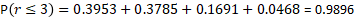
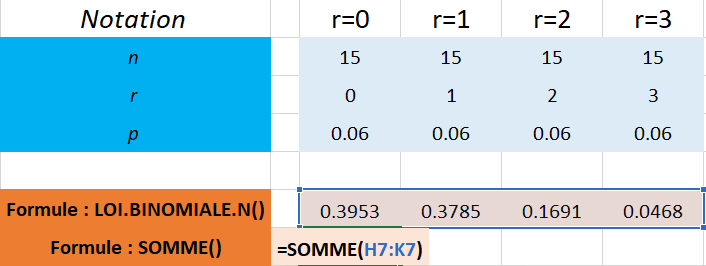
Application avec Excel :
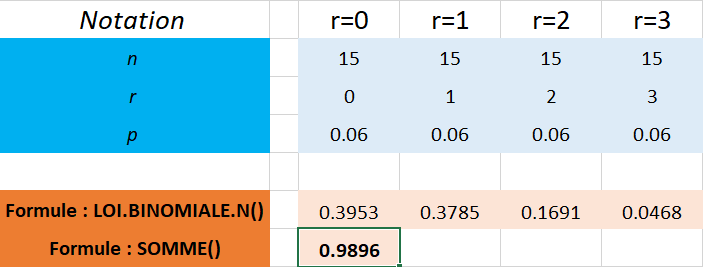
Question n°4 : Quelle est la probabilité d'observer au moins 2 pièces défectueuses dans un tel échantillon ?
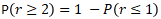
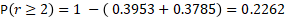
Application avec Excel :
Exemple 2 : Application de la loi de Poisson en contrôle par échantillonnage
L'entreprise “Lesmeilleurespièces” a mis en œuvre un plan de contrôle pour vérifier des lots de taille d'environ 2000 unités.
Question n°1 : En admettant qu'il y a 3 % de produit défectueux dans le lot, quelle est la probabilité d'observer 2 produits défectueux dans un échantillon de taille n = 100 ?
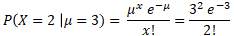
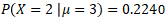
Question n°2 : Même question pour n=60 ?
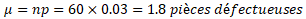
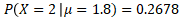
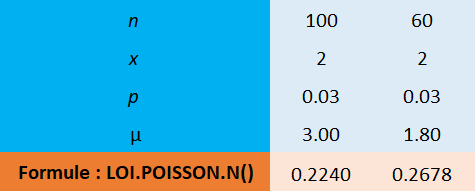
Avec Excel il est facile de réaliser les calculs avec la formule LOI.POISSON.N()
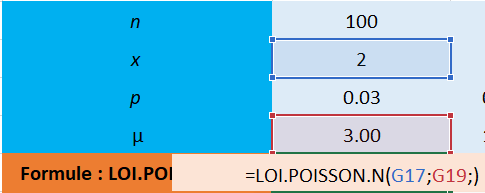
Voici le résultat obtenu pour les 2 situations :
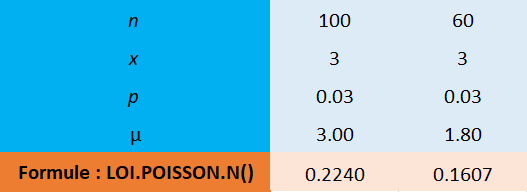
En admettant qu'il y ait 3 % de produit défectueux dans le lot, quelle est la probabilité d'observer au plus 3 produits défectueux dans un échantillon n=100 ?
Question n°3 : dans un échantillon avec n=60 ?

Voici le résultat obtenu pour les 2 situations :
Comparaison des probabilités d'acceptation des lois Binomiale et de Poisson
Comparaison des valeurs
Exemple
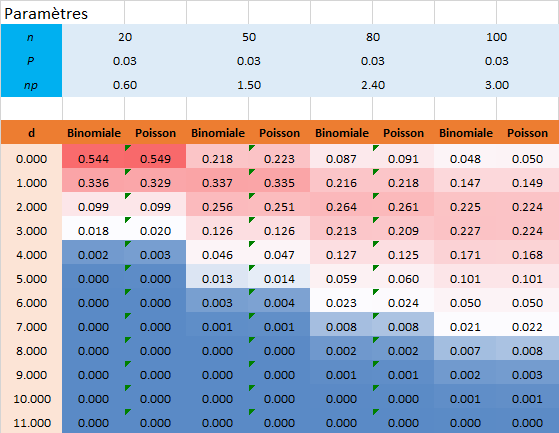
Supposons que l'on prélève dans des lots de 1000 pièces, les échantillons suivants avec des qualités effectives telles qu'indiquées dans le tableau. Comparons avec les lois binomiales et de Poisson les probabilités d'observer des défectueux dans chacun des cas.
Dans l'exemple ci-dessous, on fait l'hypothèse que le lot est composé de 3% de pièces non-conformes. Seule la taille du prélèvement change. Les probabilités calculées avec la loi binomiale et la loi de Poisson sont placées l'une à côté de l'autre. Dans la première ligne de la première colonne, on lit que dans l'échantillon de 20 pièces nous avons 54 % de chance de trouver 0 produit non-conformes. Dans la seconde ligne de la première colonne, on lit que dans l'échantillon de 20 pièces nous avons 33% de chance de trouver 0 produit non-conformes.
Calcul des probabilités avec Excel
Les illustrations ci-dessous montrent comment le calcul sous Excel a été réalisé.
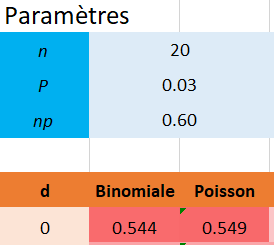
Les deux premières valeurs du tableau s'obtienne avec les formules de la loi normale et la loi de poisson. On remarquera que les paramètres utilisés diffèrent.


Probabilités cumulées
Il est également possible de calculer les probabilités cumulées pour chaque valeur correspondante de d. En supposant que les lots sont acceptables si les échantillons prélevés contiennent au plus le nombre de défectueux indiqué en première colonne, nous obtenons le tableau ci-après :
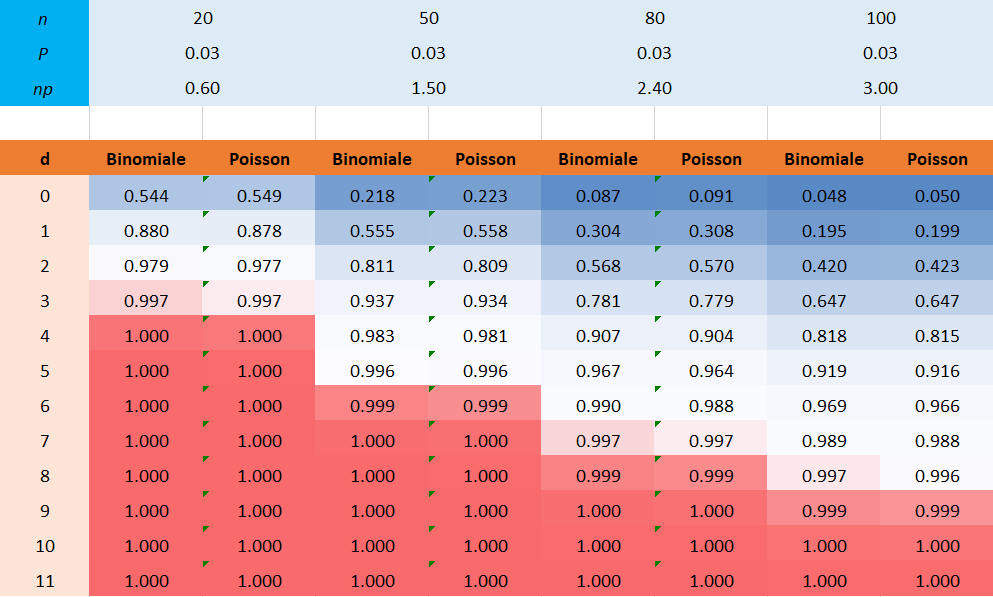
Dans ce nouveau tableau les probabilités sont cumulés. C'est-à-dire que, par exemple, pour le calcul de la probabilité, on fera la somme de 0,5438 + 0,3364 ce qui est égale à 0,8802. À mesure que la taille de l'échantillon augmente les probabilités d'acceptation selon la loi de Poisson s'approche de plus en plus de celle obtenue avec la loi binomiale. La loi de Poisson donne donc une bonne approximation lorsque la taille de l'échantillon dépasse 20.
Dans Excel, le calcul est très simple, il suffit juste de modifier le dernier paramètre par VRAI au lieu de FAUX.

Cela fonctionne aussi bien pour la loi binomiale que pour la loi de Poisson car le paramètre cumulatif est présent dans les deux fonctions.
Le plan d'échantillonnage simple
Un plan d'échantillonnage simple est caractérisé par deux nombres :
- n la taille de l'échantillon
- c le critère d'acceptation.
La méthode de contrôle est la suivante : On veut contrôler un lot de pièces identiques d’effectifs N. Un échantillon de taille n est prélevé au hasard dans ce lot. Les n pièces sont contrôlées une à une et le lot est accepté si le nombre de pièces défectueuses dans l'échantillon ne dépasse pas le critère d'acceptation c. Sinon le lot n'est pas accepté.
Efficacité d'un plan d'échantillonnage
Quels sont les risques d'erreur encourus par l'utilisation d'un plan particulier ?
Peut-on déterminer la probabilité d'acceptation d'un lot soumis au contrôle ?
L'entreprise qui utilise un plan d'échantillonnage veut bien prendre des risques, mais des risques calculés. C'est-à-dire des probabilités d'acceptation d'un lot pour la qualité effective du lot qui s'obtiennent à l'aide de la courbe d'efficacité.
Qualité effective d'un lot
On appelle qualité effective d’un lot, la proportion de pièces défectueuses ou de pièces non-conformes qu'il contient.
Courbe d'efficacité d'un plan d'échantillonnage
La courbe qui représente les probabilités d'acceptation d’un lot en fonction de la qualité effective du lot s'appelle courbe d'efficacité du plan d'échantillonnage.
Cette courbe s’obtient donc en traçant sur un graphique la probabilité de l'acceptation du lot (que nous notons Pa) en fonction de la proportion présumée de pièces non-conformes que nous notons p dans le Lot.
La proportion d'individus non-conformes p dans un lot peut varier de 0 à 100 %. Les plans de contrôle sont généralement accompagnés de leur courbe d'efficacité. Il s'agit alors d’associer la probabilité d'acceptation Pa d’un lot pour différentes valeurs de p, la proportion défectueuse présumée dans le lot. Cette courbe va nous permettre de juger de la puissance discriminatoire prélèvement.
Notation dans le contexte du contrôle qualité :
- N: Taille du lot
- n : Taille de l'échantillon
- c : Critère de décision
- p est la probabilité de succès à un essai
Exemple
On décide de prendre pour exemple les contexte suivant : Le responsable du contrôle qualité à réception reçoit un lot de taille 5000 dans lequel il prélève un échantillon de 80 pièces et sur lequel on applique une limite d'acceptation à 2.
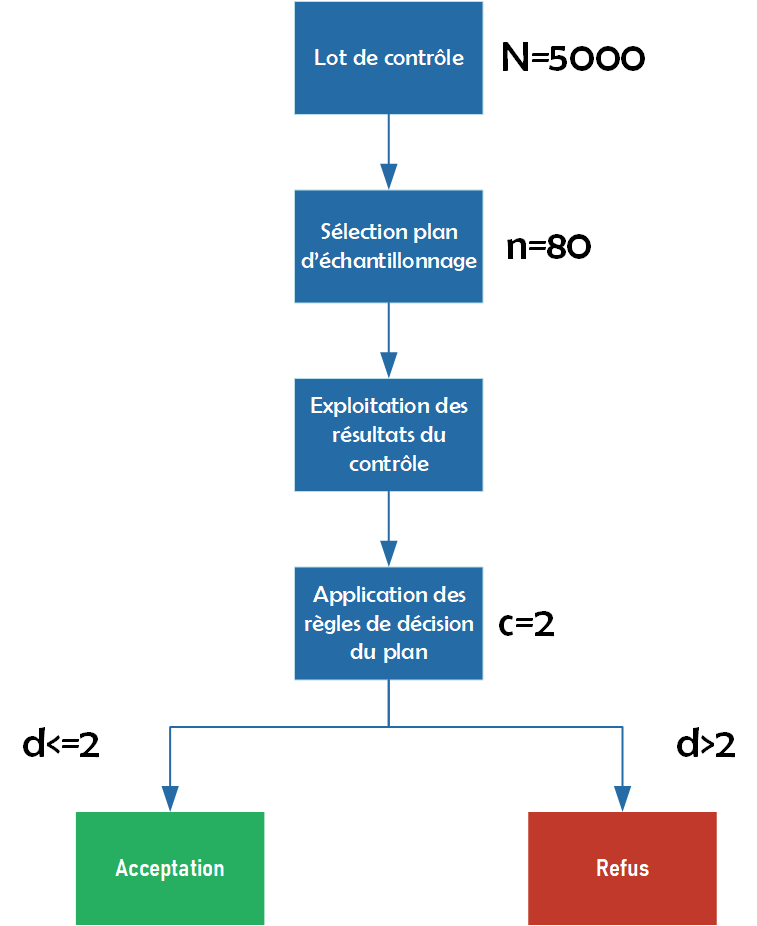
La probabilité d'acceptation dépend de la qualité effective du lot qui le reçoit. La courbe d'efficacité expliquée ci-dessous permet de faire le lien entre ces deux paramètres.
Tableau d'efficacité
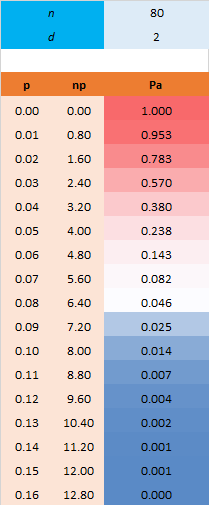
La probabilité d'acceptation dépend de la qualité effective du lot qu'il reçoit. La courbe d'efficacité expliquée ci-dessous permet de faire le lien entre ces deux paramètres.
Courbe
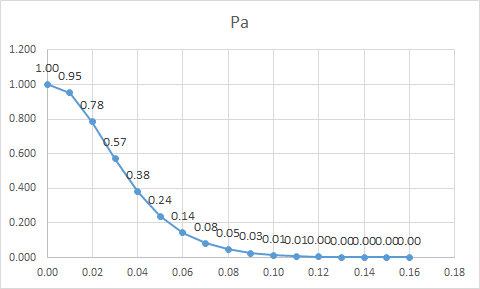
Le tracé de la courbe d'efficacité nous indique la variation de la probabilité d'acceptation d'un lot en fonction de sa qualité effective.
La courbe ci-dessus nous permet de faire les constats suivants
Les lots comprenant 2 % de pièces non-conformes sont acceptés 78 fois sur cent Pa = 0,78 en moyenne.
Les lots contenant 8 % de pièces non-conformes sont acceptés 5 fois sur cent.
Comment rendre plus discriminatoire une courbe d'efficacité ?
La courbe d'efficacité d'un plan d'échantillonnage simple dépend de n de c
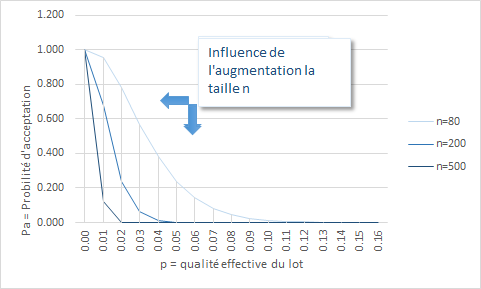
Effets de la variation de N sur la courbe d'efficacité.
Pour une même valeur de c, plus la valeur de n est élevée plus la courbe d'efficacité décroît rapidement donnant ainsi une meilleure sélectivité au contrôle. Il est toutefois accompagné d'un coût de contrôle plus élevé.
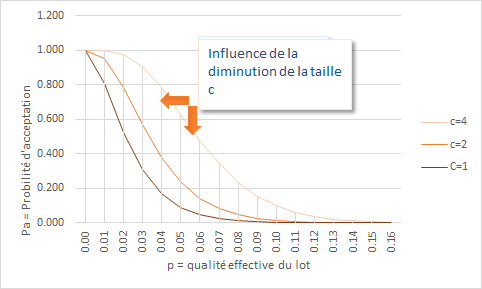
Effet de la variation de c sur la courbe d'efficacité.
Pour une même taille d'échantillon, une diminution du critère d'acceptation rend la courbe plus discriminatoire.
La courbe d'efficacité devient alors moins aplatie indiquant un contrôle plus sévère.
Courbe d'efficacité idéale
La courbe d'efficacité idéale est celle qui donne une discrimination parfaite entre les bons lots et les mauvais lots. Imaginons une situation où il est accepté uniquement les lots ayant moins de 5 % de produit non-conformes. La courbe idéale est une courbe pour laquelle la probabilité d'acceptation est de 100 % des lots compris entre 0 et 5% de produit non-conforme et une probabilité d'acceptation de 0 % des lots ayant plus de 5 % de produits non-conforme. Pour obtenir une telle courbe, il est nécessaire de faire un contrôle de 100 % des effectifs.
Choix d'un plan d'échantillonnage
Lorsque nous contrôlons un certain lot, certaines questions se posent :
- Quelle taille d'échantillon doit-on prélever ?
- Combien de pièces défectueuses allons-nous tolérer dans l'échantillon avant de ne pas accepter le long ?
Idéalement, nous aimerions établir un plan d'échantillonnage qui va refuser tous les mauvais lots et est accepter tous les bons lots. Mais on ne peut s'attendre à ce qu'un plan d'échantillonnage nous donne de tels résultats.
Le recours aux plans d'échantillonnage induit nécessairement un risque.
On doit considérer les risques encourus à l'aide de la courbe d'efficacité.
Pour que la courbe d'efficacité correspondent aux risques que l'on veut encourir, il faut considérer quatre éléments :
- le niveau de qualité acceptable
- le niveau limite de qualité toléré
- le risque fournisseur
- le risque client
Niveau de qualité acceptable (AQL/NQA)
Un lot de qualité acceptable est caractérisé par un certain pourcentage d'individus non-conformes que l'on peut tolérer que l’on notera NQA et qui a une forte probabilité d'acceptation.
C'est la norme qualité que nous imposons. Il s’agit du niveau de qualité que peut produire un processus maîtrisé. Ce pourcentage d’individus non-conformes aura une forte probabilité d'acceptation.
C'est ce que l'on entend par un bon lot.
On utilise également dans la littérature la notation AQL : Acceptable Quality Level pour identifier le niveau de qualité acceptable. Cette notation est très répandue dans les entreprises.
Le niveau limite de qualité toléré (LTPD/LQ)
Le niveau limite de qualité toléré que nous notons par LTBD représente le pourcentage d'individus non-conformes dans un lot qui devrait avoir très peu de chance d'être accepté en moyenne.
LTBD représente le pourcentage de pièces non-conformes que contient un très mauvais lot. On utilise également la notation LQ (limite de qualité). Quels sont maintenant les risques de ne pas accepter un bon lot et d'accepter un mauvais lot ? Un bon lot est associé le risque fournisseur et un mauvais le risque client.
risque du fournisseur α
Le risque du fournisseur noté α est la probabilité de ne pas accepter un lot de qualité acceptable de niveau NQA. α représente donc les chance sur 100 qu'un lot de qualité acceptable ne soit pas accepté par le plan d'échantillonnage. C'est le risque de première espèce que nous utilisons dans un test statistique et qui représente la probabilité de ne pas accepter l'hypothèse nulle H0 lorsqu'elle est vrai
le risque clientβ
Le risque client noter β est la probabilité d'accepter un lot de qualité inacceptable, c'est-à-dire de niveau LTBD. β représente donc les chances sur 100 qu'un lot de qualité inacceptable soit accepté par le plan d'échantillonnage. C'est le risque de deuxième espèce dans un test statistique qui représente la probabilité d'accepter l'hypothèse nulle H0 lorsque en réalité elle est fausse.
Cela est couramment représenté de la façon suivante :
| Réalité | |||
| H0 est vrai | H1 est vrai | ||
Décision |
H0 est accepté | Ok | Risque β: Risque client |
| H1 est accepté | Risque α: Risque fournisseur | ok | |
Enjeux de l'échantillonnage
Il est évident que l'on veut un plan d'échantillonnage qui aura une forte probabilité d'acceptation pour les bons lots et une faible pour l'acceptation des mauvais lots.
Imaginons la situation suivante :
- NQA = 2%
- LTPD = 8%
- le risque fournisseur &alpha ; = 0.05
- le risque client &bêta ; = 0.08
| Réalité | |||
| H0 est vrai | H1 est vrai | ||
| Décision | H0 est accepté | 95% | Risque β: 10% |
| H1 est accepté | Risque α: 5% | 90% | |
Ayant fixé ces conditions on peut alors dire que le plan d'échantillonnage devrait accepter 95 fois sur cent en moyenne les lots dont la qualité est 2 % ou meilleur et qu'il devrait accepter seulement 10 fois sur 100 en moyenne les lots dont la qualité est 8 % au pire. Ces données peuvent se représenter aisément sur la courbe d'efficacité. La courbe d'efficacité du plan d'échantillonnage passe par ces deux. L'allure de la courbe dépendra également de deux autres paramètres qui sont n et c.
Les tables d'échantillonnage
MIL-STD-105 était une norme de défense des États-Unis qui fournissait des procédures et des tableaux d'échantillonnage par attributs basés sur les théories d'inspection d'échantillonnage de Walter A. Shewhart, Harry Romig et Harold Dodge et sur des formules mathématiques. Cette norme a été largement adoptée en dehors des applications d'approvisionnement militaire.
La table de J. M. CAMERON
Cameron JM (1952).Tables for constructing and computing the Operating Characteristics of Single Sampling Plans. Industrial Quality Control. Vol.11, pp.37 - 39.
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT
