Estimation de paramètres
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
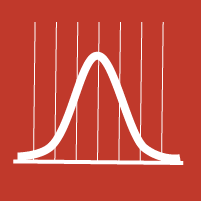 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
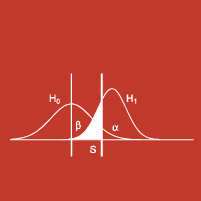 Tests statistiques
Tests statistiques
Estimation, estimateur, critère
On va voir dans ce dossier comment estimer la moyenne d'une population, un pourcentage de population et la variance d'une population. Bien sûr, ces estimations ne correspondront jamais aux valeurs exactes des paramètres de la population. Les erreurs sont inévitables lorsqu'il s'agit d'estimation, mais vous allez voir que l'importance de ces erreurs peut être évaluée et contrôlée.
Faire une estimation implique nécessairement d'accompagner une proposition d'un degré de confiance.
Une estimation : Une estimation est une valeur spécifique ou une quantité obtenue pour une statistique telle que la moyenne de l'échantillon, le pourcentage de l'échantillon, la variance de l'échantillon.
L'estimation est également un processus qui consiste à produire une estimation d'un paramètre de la population.
Un estimateur : Un estimateur est une statistique qui est utilisé pour estimer un paramètre.
Par exemple la moyenne de l'échantillon x est un estimateur de la moyenne μ. Voir tableau ci-dessous :
| Correspondance | Population | Echantillon |
|---|---|---|
| Moyenne |
μ
|
x |
| Variance |
α2 |
s2 |
| Ecart-type |
α |
s |
| Taille | N |
n |
| Pourcentage | π |
p |
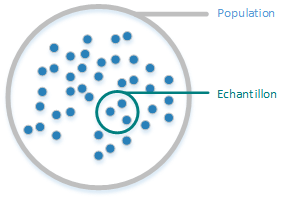
Un estimateur sans biais : Un estimateur sans biais est un estimateur pour lequel la distribution d'échantillonnage a une moyenne qui est égale au paramètre de la population qui est estimé.
Les 2 types d'estimation
L'estimation ponctuelle
L'estimation ponctuelle est une estimation où l'estimateu est un simple nombre utilisé pour estimer un paramètre de population.
L'estimation par intervalle
L'estimation par intervalle est une estimation où l'estimateur est une étendue de valeur utilisée pour estimer un paramètre de population.
En effet, il est assez exceptionnel, par exemple, que la moyenne d'un échantillon soit exactement égale à la moyenne de la population.
Quel type d'estimation choisir ?
L'estimation ponctuelle le sera presque tout le temps fausse et surtout ne laissera pas présager de la précision de l'estimation. A la différence de l'estimation par intervalle qui donnera une étendue qui contiendra le paramètre de la population. Dans ce cas, l'erreur d'échantillonnage sera intégrée dans l'intervalle. La précision de l'estimation est donc quantifiée. Bien sûr, une estimation par intervalle peut être fausse, mais, à la différence de l'estimation ponctuelle le, la probabilité d'erreur de l'intervalle peut être déterminé.
Estimation par intervalle
La largeur de l'intervalle
Un intervalle de confiance est un intervalle de valeurs à l'intérieur duquel la valeur exacte se trouve probablement.
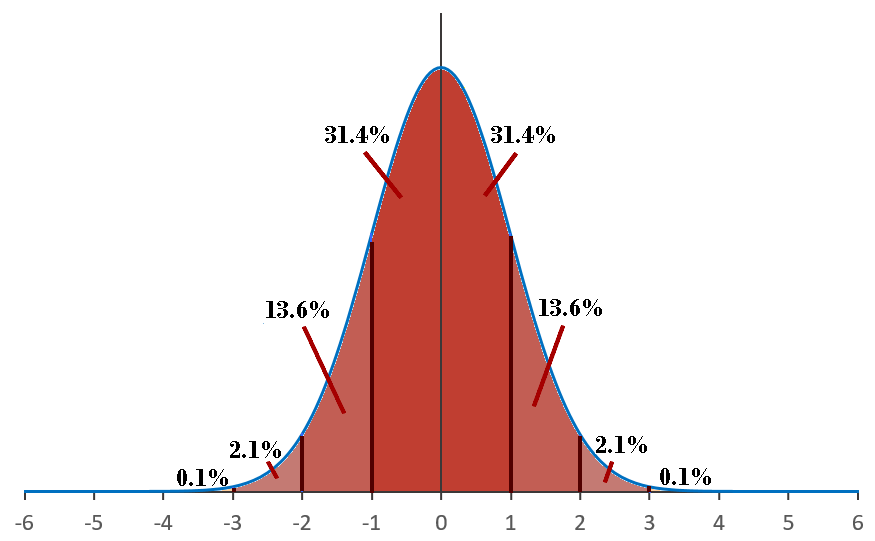
L'amplitude de l'intervalle caractérise la précision de l'estimation. Si l'on est, dans le cas où la taille d'échantillonnage est suffisamment grande pour que la distribution d'échantillonnage suive une loi normale, on peut affirmer que 95.4% des moyennes des échantillons se situeront à ±2σx de μ.
On peut également faire l'affirmation inverse, si nous avons un échantillon qui a une moyenne x alors la moyenne μ de la population sera se situera à ±2σx de x.
Fiabilité et précision
Prenons l'exemple suivant :
La population possédant une cafetière à capsule se situe entre 27% et 33% de la population avec un risque de 5%.
- La fiabilité est représentée par le chiffre de (5%) soit 95%
- La précision est représentée par l'intervalle (33%-27%) soit 6%
Estimation d'une moyenne inconnue
Pour estimer une moyenne inconnue, je vous invite à consulter notre dossier sur le théorème central limite qui explique de façon détaillée comment faire une telle estimation.
Le risque d'erreur consenti α
Par convention, jusqu'à présent, nous avons estimé les intervalles de confiance des moyennes à 95 %, c'est-à-dire un risque d'erreur de 5 %. On appelle risque d'erreur α. En fonction des situations, il est possible de choisir un risque d'erreur différent de 5 %.
Pour chaque valeur de risque α il existe une correspondance de la valeur Z
| α | Z |
|---|---|
| 5% | 1.96 |
| 2% | 2.33 |
| 1% | 2.58 |
| 0.1% | 3.3 |
Si nous choisissons un risque d'erreur plus faible, cela implique automatiquement en élargissement de l'intervalle de confiance et donc d'une estimation moins précise.
Détermination de la taille de l’échantillon
Précision d'une estimation
La précision d'une estimation dépend du risque alpha α et de la taille n de l'échantillon.
Influence du risque alpha
Plus de risque alpha et petit plus la valeur Z est grande et plus l'intervalle de confiance est grand.
Influence de la taille de l'échantillon
La taille de l'échantillon intervient dans la formule qui détermine l'écart-type de la moyenne.
Rappel du calcul de l'écart-type de la moyenne (Théorème central limite)
l'écart-type de la moyenne m est égal à l'écart-type des valeurs de l'échantillon population divisé par la racine carrée de la taille d'échantillon.
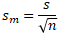
En conséquence, plus la taille de l'échantillon est grandes plus l'écart-type de la moyenne est petit, plus l'intervalle de confiance sera serré.
Cela permettra une plus grande précision.
Détermination de la taille de l'échantillon
Pour une estimation de moyenne
Afin de déterminer la taille de l'échantillon la formule suivante pourra être utilisée :
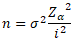
Zα sera généralement égale à 1.96.
La variance σ2 de la variable quantitative étudiée dans la population est souvent estimée d'après des études antérieures sur le même sujet.
La valeur i est la précision désirée, c'est-à-dire la moitié de l'intervalle de confiance.
Les lois statistiques
Des lois statistiques régissent les différents paramètres statistiques issus de l'échantillonnage telle que :
- la loi de Student pour les moyennes
- la loi du Chi2 pour les écarts type
- la loi de Fisher pour le quotient de deux variances
- la loi binomiale pour les proportions.
Choisir la loi qui convient pour traiter les résultats des échantillons est nécessaire mais dans certains cas il est possible d'utiliser des lois différentes Par exemple :
- une loi normale à la place d'une loi de Student
- une loi normale à la place d'une loi binomiale
- une loi de Poisson à la place d'une loi binomiale
- une loi normale à la place de la loi de Poisson
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT
