Les distributions statistiques
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
 Tests statistiques
Tests statistiques
Qu'est-ce qu'une distribution ?
Une distribution est une fonction qui associe une fréquence d'apparition à une classe de valeur. Cette fonction permet de résumer l'information contenue dans un ensemble de données.
Une distribution n'est pas un graphique. Une distribution est souvent associée à un graphique, mais n'en est pas un. Cette erreur est très répandue. Nous verrons plus loin quelles en sont les raisons.
Le premier type de représentation est sous forme de tableau.
Les représentations graphiques sont toutefois idéales pour se représenter les fréquences.
Distribution de fréquences relatives et distribution de probabilité
La distribution de fréquences
relatives comptabilise le nombre de fois qu'un "événement" d'intérêt intervient. Il se base sur des observations.
- Exemple : Par exemple on lance 100 fois un dé et on compte combien de fois chaque face apparaît.
La distribution de probabilité, elle, permet d'approximer la distribution de fréquences d'une population qui est étudiée. Elle n'est pas le fruit d'observations.
Souvent, la distribution des valeurs d'un échantillon est proche de modèles mathématiques. Ces modèles sont appelés "modèles de distribution de probabilité" ou encore "loi de distribution de probabilité".
Distribution de fréquences relatives
Exemple de variable discrète : Distribution des classes d'âges
Une enquête est réalisée auprès de 1000 individus Hommes qui ont été interrogés au sujet de leur classe d'âge. Ces individus ont été choisis au hasard sur l'avenue des Champs Elysée. Cette enquête donne le jeu de donnée suivant ci-dessous.
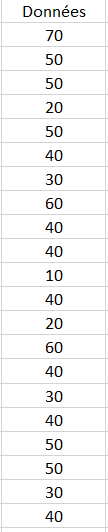
Vous avez ici un extrait des 21 premières valeurs.
Pour réaliser l'enquête, la classe d'âge a été déterminée à partir de l'âge des individus. Ainsi, une personne ayant 52 ans appartient à la classe d'âge 50. La variable classe d'âge est une variable discrète , car il y a une rupture entre les différentes classes d'âge.
Questions :
"Quelle est la probabilité que si nous interrogions une nouvelle personne, sa classe d'âge soit 30 ?"
Grâce à notre connaissance de la distribution, nous pourrons répondre à cette question.
Représentation de la distribution sous forme de tableau :
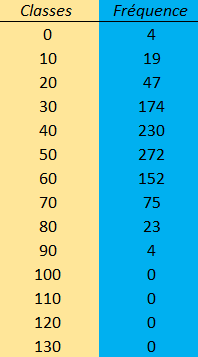
A partir du jeu de données, on peut établir le tableau de fréquence ci-dessus simplement en dénombrant les individus appartenant à chaque catégorie. Ici, on peut clairement observer l'association d'une fréquence à une classe de valeur.
Il est possible à partir de ce moment de déterminer la fréquence relative (C'est-à-dire une probabilité). Cette probabilité est calculée en faisant le rapport entre la fréquence et l'effectif total de la population. p(x)=ni/N
Par exemple pour la classe d'âge 50, on fera le calcul : 272/1000 = 0.272.
On fera de même pour chaque ni.
Ce résultat est arrondi à 0.3 dans le tableau suivant :
A partir cette distribution il est possible de répondre à la question soulevée plus haut : "Quelle est la probabilité que si nous interrogions une nouvelle personne, sa classe d'âge soit 30 ?" La réponse sera 0.174, On pourra alors affirmer que nous avons environ 20% de chance que cette personne soit de la classe d'âge 30.
A partir de maintenant vous pouvez toucher du doigt la puissance des statistiques qui permettent de présager d'un résultat avant même d'en d'avoir fait une expérience. Grâce à ce tableau, si vous deviez miser $10 sur la classe d'âge de la prochaine personne interrogée vous miseriez sur la classe d'âge 50 car c'est elle qui a la probabilité d'occurrence la plus grande dans notre exemple.
Représentation de la distribution sous forme de graphique
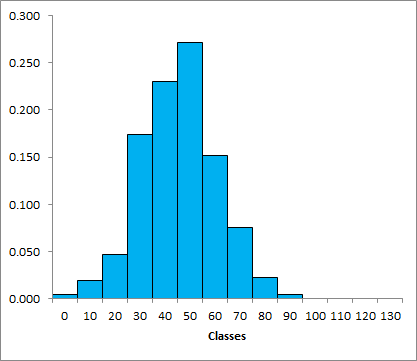
La distribution d'une variable discrète se représente sous forme de graphique en barres. Cela est possible, car il n'y a qu'un nombre limité et fini de catégories.
Variable continue
Exemple de variable continue: Distribution des poids
Le poids de 1000 individus est recueilli et donne le jeu de données suivant ci-dessous.
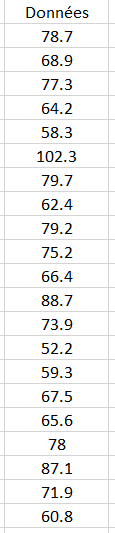
Vous avez ici un extrait des 21 premières valeurs. On remarquera tout de suite qu'il s'agit de variables continues.
Maintenant, je vous pose la question suivante :
"Quelle est la probabilité que si nous interrogions une nouvelle personne, son poids soit égale à 60 kg ?"
C'est grâce à notre connaissance de la distribution que nous pourrons répondre à cette question.
Représentation de la distribution sous forme de tableau:
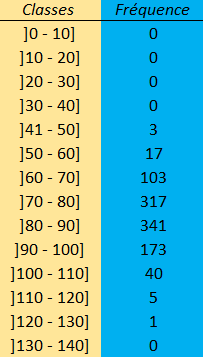
Le regroupement en classe d'une variable continue engendre une perte d'information. Pour pallier à cela, il est possible de diminuer l'amplitude des classes et donc, donc d'augmenter leur nombre.
La représentation ci-dessous indique une amplitude de classe de a=10.
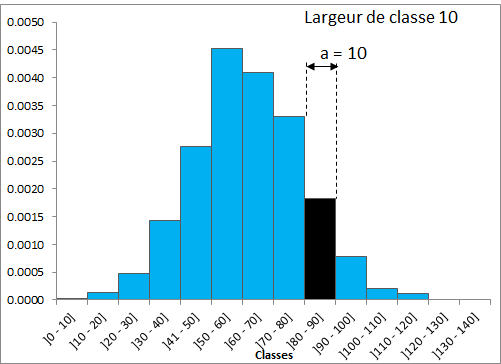
Cela se traduit par une diminution de la hauteur et de la largeur des barres. En revanche la somme des fréquences relative dans l'air total de l'histogramme est toujours égal à 100 % .
Pour pallier ce problème, il faut diviser la probabilité p(x) par l'amplitude de la classe a soit la largeur du rectangle. f(x)=p(x)/a
L'air de chaque rectangle représente toujours la fréquence relative de la classe et F de X est appelée densité de fréquence relative.
Représentation de la distribution sous forme de ligne continue:
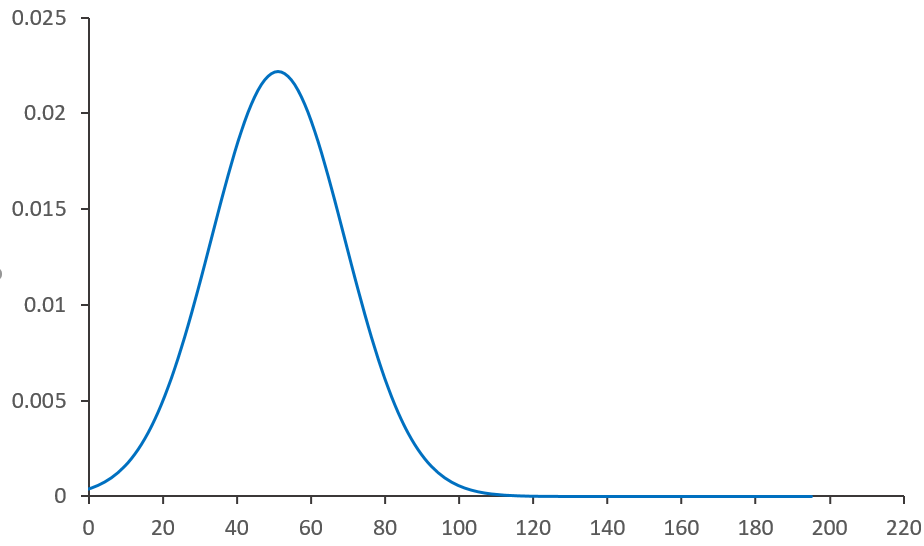
Comme nous l'avons vue, si on augmente le nombre de classes, la représentation d'une distribution d'une variable continue se présente sous la forme d'une ligne continue. Au delà d'un certain nombre de classes, il n'est pas possible de représenter la distribution de cette variable sous forme de barre.
Cette ligne s'appelle la fonction de densité de probabilité.
Propriétés
Nous pouvons tirer des propriétés intéressantes.
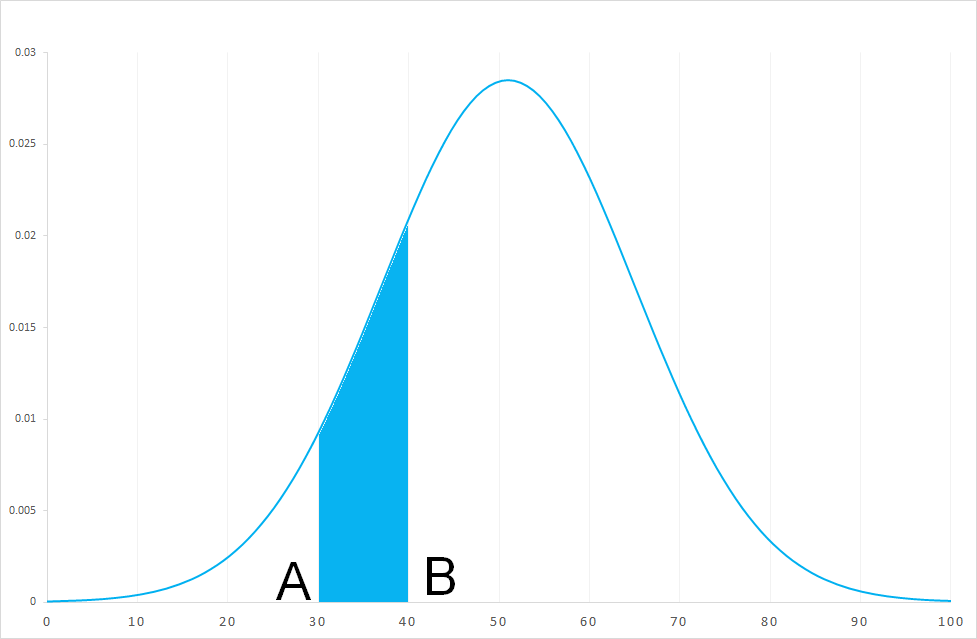
- L'air contenu sous la courbe entre deux valeurs A et B représente la probabilité que X soit comprise entre A et B.
- L'air contenue sous la courbe avant une valeur représente la probabilité que X soit inférieur à A. L'air contenu sous la courbe après une valeur B représente la probabilité que X soit supérieur à B.
- L'aire sous la courbe représente la somme totale de toutes les probabilités de chaque valeur de la variable X elle est égal à 1.
Si l'on souhaite connaître la probabilité associée au poids de 60kg, on ne peut pas juste lire la valeur associée :
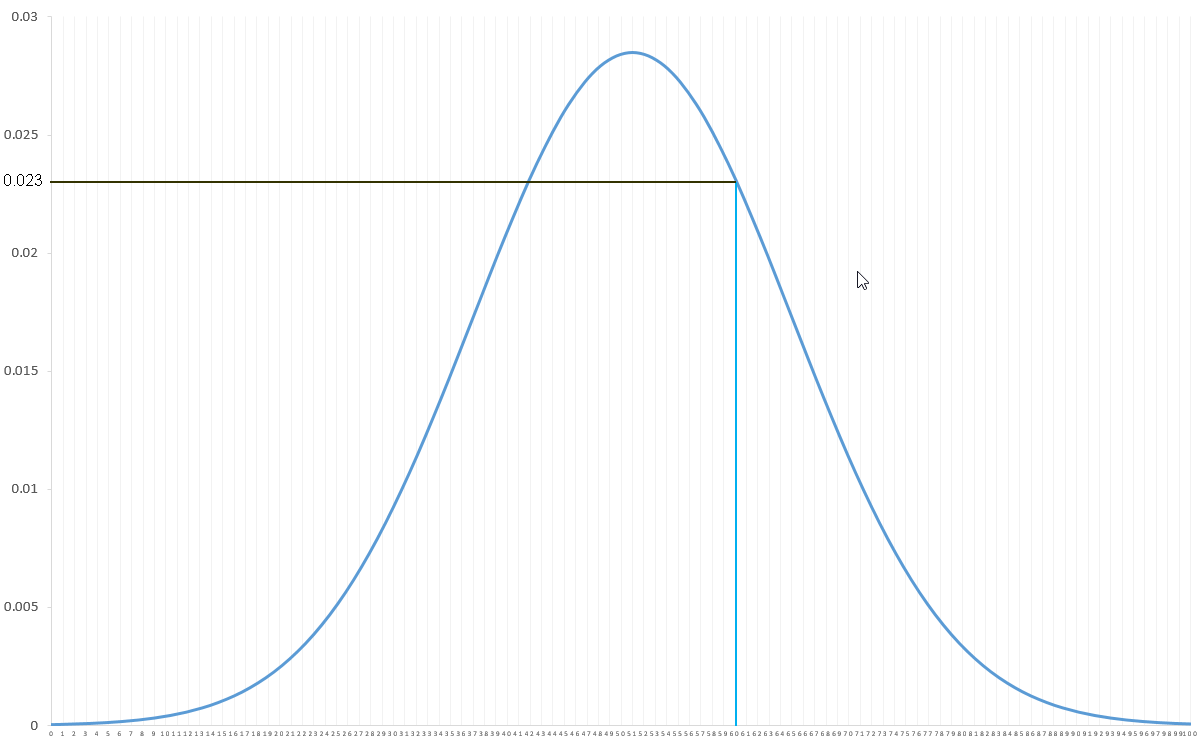
En effet, il n'y a pas 23% de personnes qui ont exactement un poids de 60kg. La probabilité qu'une personne sélectionnée au hasard fasse exactement 60kg est quasiment de 0.
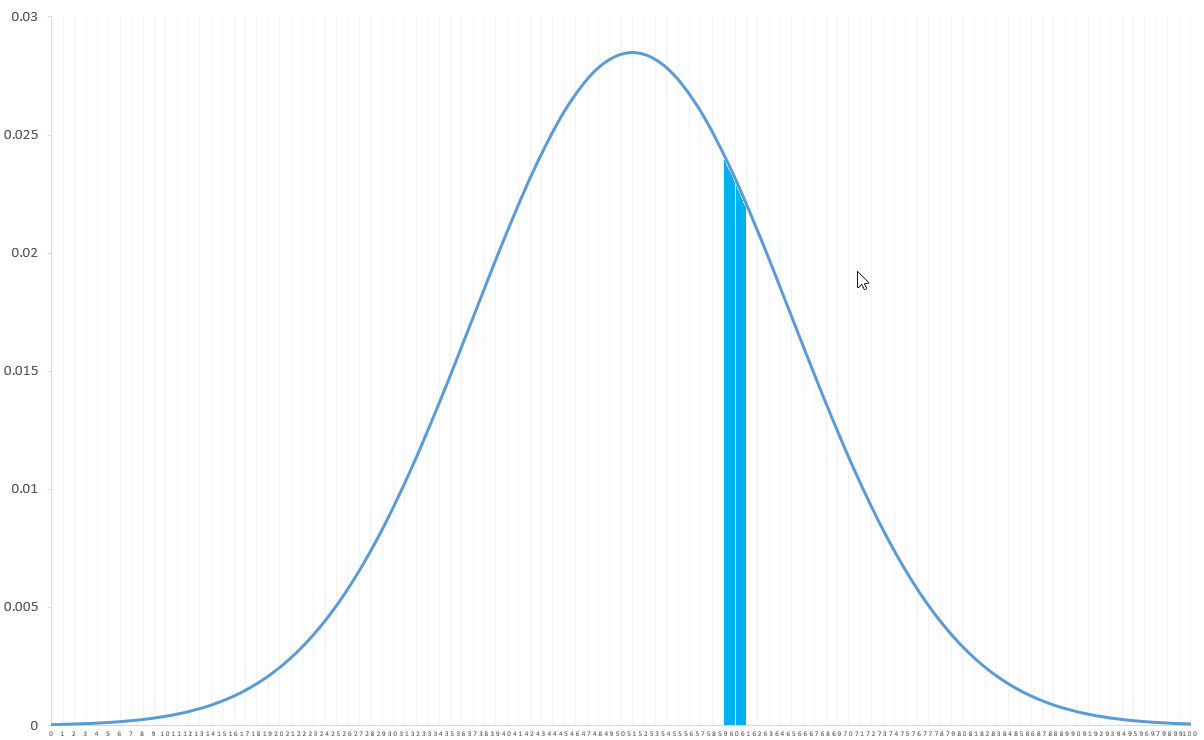
Pour pallier ce problème, il est possible de changer légèrement l'énoncé du problème et au lieu de spécifier une valeur précise, préciser plutôt une plage de valeurs. Dans le cas suivant l'aire entre 59 et 61 : P (59<x<61). Dans une situation avec des variables continues, les probabilités sont représentées par les aires en-dessous de la courbe. Plus l'aire sera grande plus la probabilité sera grande.
Ce calcul pourra se faire en obtenant les valeurs grâce aux tables de la loi normale. Vous pouvez vous référer au dossier loi normale .
Pour aller plus loin consulter également le site qui constitue une importante source de connaissance : http://onlinestatbook.com/
Les lois de distribution de probabilités
Théoriquement il existe une infinité de modèles de distribution. Les lois de probabilité se distinguent par :
- leurs formes
- leurs paramètres de position
- leurs paramètres de dispersion
Pour déterminer le modèle que suit un processus, il faut exploiter les informations contenues dans l'échantillon grâce à des méthodes statistiques.
Une fois que le modèle est déterminé, il est utilisé pour prédire les propriétés de l'ensemble de la population. Dans toute prévision il existe différents degrés de précision. Plus la taille de l'échantillon est grande meilleure est la précision.
Les distributions ont des fonctions de densité de probabilité qui leur sont attachées. Elles constituent des lois qui permettent de décrire la manière avec laquelle sont distribuées les valeurs.
Une distribution de probabilités est simplement une énumération de tous les résultats possibles d'une expérience avec leurs probabilités respectives. Par exemple, le résultat d'un lancé de dés est soit 1,2,3,4,5, ou 6. Ces chiffres correspondent aux résultats possibles. Pour chacun de ces chiffres on associera une probabilité.
La même logique peut être employée pour déterminer les probabilités relatives des résultats de 2 lancés de dés.
Pour réaliser cette étude il faut d'abord énumérer dans un tableau les résultats possibles :
| Résultats | Probabilité |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| Total |
Puis on associe les probabilités
| Résultats | Probabilité |
|---|---|
| 2 | 1/36 |
| 3 | 2/36 |
| 4 | 3/36 |
| 5 | 4/36 |
| 6 | 5/36 |
| 7 | 6/36 |
| 8 | 5/36 |
| 9 | 4/36 |
| 10 | 3/36 |
| 11 | 2/36 |
| 12 | 1/36 |
| Total | 36/36=1 |
Dans le tableau ci-dessus tous les résultats possibles sont listés. On notera que la somme de toutes les probabilités est égale à 1.
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT

