
Mesure et incertitude de mesure
Contenu de la page
Les processus de mesure ont leur propre variabilité. Le résutlat d'une mesure ne correspond jamais à une réalité absolue. Il permet seulement d'approcher cette réalité.
La maîtrise des processus de mesures est indispensable à la prise de décision en entreprise.
Maîtriser les processus de mesure ne signifie pas pour autant rechercher une précision extrême pour toutes les mesures. Il s'agit d'obtenir des résultats avec un niveau de confiance adaptés aux besoins.
La variabilité de mesure
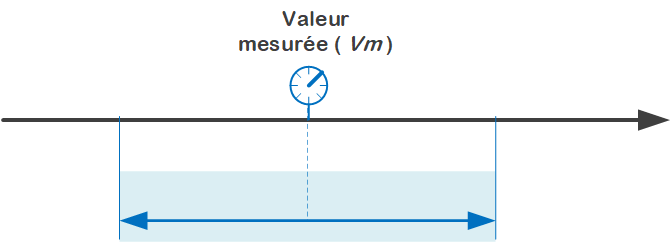
Il faut savoir que les processus de mesure ont leur propre variabilité. La mesure ne correspond jamais à une réalité absolue. La mesure permet seulement d'approcher cette réalité.
Note : Le processus de mesure est composé de facteurs indépendants, on peut donc admettre que les erreurs que produit se distribuent en suivant la loi normale .
Incertitudes de mesures et erreur de mesure
L'erreur de mesure
Il faut bien faire la différence entre l'erreur de mesure et l'incertitude de mesure. L'erreur de mesure correspond à l'écart entre la valeur vraie et la valeur mesurée.
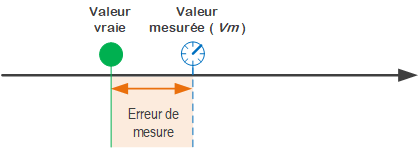
"Erreur de mesure : différence entre la valeur mesurée d'une grandeur et une valeur de référence"
Note : Ici la valeur de référence est la valeur d'une grandeur servant de base de comaraison pour les valeur de grandeur de même nature. La valeur de référence, peut être, dans certain cas, la valeur vraie d'un mesurande.
L'incertitude de mesure est la dispersion des valeurs pouvant être attribuée au mesurande.
Notation :
- Vm: Valeur mesurée
- U: Incertitude de mesure
On exprimera le résultat de la façon suivante : Vm ± U.
Par exemple, le poids relevé sur le pèse-personne pourra être exprimé ainsi : 81.2±0.3 Kg.
Le résultat d'une mesure peut s'exprimer comme suit :
Résultat de mesure = valeur vraie + erreur de mesure
La valeur vraie est la valeur que l’on obtiendrait par un mesurage parfait, C'est-à-dire sans incertitude. Autant dire que la valeur vraie est utopique. La valeur vraie sera donc toujours une inconnue que l'on cherchera à déterminer le mieux possible.
Toute personne qui prend une mesure doit toujours prendre du recul par rapport à la valeur qu'il annonce.
Incertitude de mesure
Le mot "incertitude" signifie doute. Ainsi, dans son sens le plus large "incertitude de mesure" signifie doute sur la validité du résultat de mesurage.
L'expression quantitative du concept d'incertitude de mesure est réalisée grâce à l'écart-type.
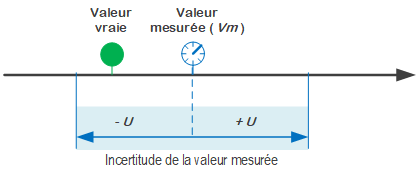
On observe régulièrement que si l'on fait plusieurs fois une même mesure, on observe des résultats qui diffèrent entre eux. Il y a donc une incertitude de mesure associée à chaque résultat. L'incertitude nommée U est représentée par une plage de valeur de telle sorte qu'il y ait de fortes probabilités que la valeur vraie s'y trouve incluse.
Différence entre la variabilité d'un processus production et variabilité de la mesure.
La variabilité totale d'un processus est égale à la variabilité du processus de production plus la variabilité de la mesure :
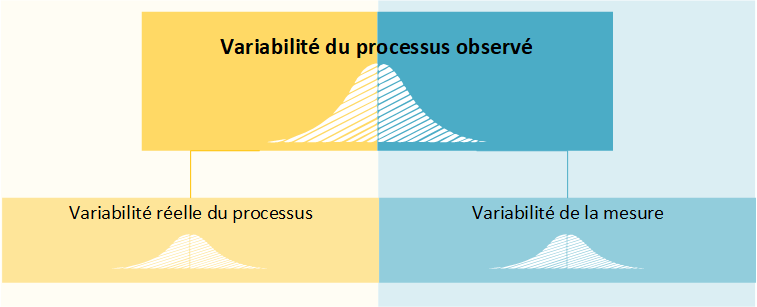

C'est pour cela que les moyens de mesures doivent être préalablement validés. Si le processus de mesure n'est pas maîtrisé, il sera impossible de prendre des décisions ou, pire encore, les décisions qui auront été prises seront erronées.
Note : Dans certains cas, une dispersion du processus de mesure importante conduit à une surestimation de la variabilité du processus de production.
Titre : Estimer l'incertitude : mesures, essais
Auteurs : Christophe Perruchet, Marc Priel
Éditeur : FeniXX
ISBN : 2402115270, 9782402115278
Longueur : 150 pages
Les référentiels
Les principaux guides en vigeur pour l'expression des incertitudes de mesure sont :
- Le GUM
- La norme NF ISO 5725
Que l'on s'appuie sur l'une ou l'autre de ces deux méthodes, le concept d'incertitude de mesure est le même, dans les 2 cas nous allons estimer les écarts-types des variables aléatoires.
Illustration par un exemple
Prenons 2 groupes de personnes dont on mesure la taille.
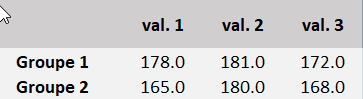

La valeur de l'écart-type expérimental est calculée dans la colonne orange. Vous retrouverez la méthode de calcul en suivant ce lien.
Ensuite, on peut obtenir les valeurs de l'estimation de l'écart-type des moyennes. Cet écart-type est donné dans la colonne jaune pour chacun des groupes. Il est égal à l'écart-type de la population divisé par la racine carrée de la taille d'échantillon. Voir le
théorème central limite
.
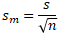
Dans notre exemple, nous diviserons les écarts types des échantillons par la racine de 3.
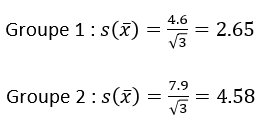

L'écart-type, calculé dans l'exemple ci-dessus, donne un intervalle probable pour une valeur xi.
Il s'agit de la même logique que pour un contrôle. On fait en générale n fois la mesure.
- La moyenne est alors calculée.
- L'incertitude (écart-type estimé de la moyenne) est alors associée à la moyenne des mesures.
Dans notre exemple, on pourra dire que la taille moyenne
- du groupe 1 est égale à 177 ± 2.65 et
- du groupe 2 est égale à 171 ± 4.58.
On exprimera par cet intervalle la plage de valeur probable.
Cas où la distribution des valeurs suit une loi normale
Si la distribution des valeurs suit une loi normale on peut alors affirmer qu'il y a 68,3 % de chances pour que la moyenne ait une valeur vraie qui soit encadrée par plus ou moins un écart-type soit :
Expression de l'incertitude : x ± s(x).
Il y a malgré tout, 31,7 % de chance que cela soit faux. Cet intervalle de confiance est, par conséquent, pas toujours suffisant. On peut alors utiliser un facteur d'élargissement K qui donnera un intervalle de confiance plus large. Le facteur k sera multiplié aux écarts-types :
Expression de l'incertitude élargie : x ± k x s(x)
Le facteur à appliquer dépend du niveau de confiance que l'on souhaite avoir.
| Facteur k | Niveau de confiance (en %) |
|---|---|
1 |
68.27 |
1.64 |
90 |
1.96 |
95 |
2 |
95.45 |
2.57 |
99 |
3 |
99.73 |
Dans notre exemple, avec un facteur k de 2, on pourra dire que la taille moyenne
- du groupe 1, il y a 95.45% de chance pour que la valeur vraie de la moyenne des résultats soit comprise dans l'intervalle suivant: 177 ± 2 x 2.65 soit 177 ± 5.3 avec
- du groupe 2, il y a 95.45% de chance pour que la valeur vraie de la moyenne des résultats soit comprise dans l'intervalle suivant: est égale à 171 ± 2 x 4.58 soit 177 ± 9.16
Lorsque l'on exprime une incertitude élargie, on doit toujours donner le facteur d'élargissement où le niveau de confiance associé.
Pour pouvoir appliquer les niveaux de confiance précédents, il faut s'assurer que les mesures suivent la loi normale, où que la taille de l'échantillon n est supérieure à 30. (Voir explication dans le dossier théorème central limite )
Cas ou la distribution des valeurs suit une loi de student
La distribution de Student ressemble à une loi normale aplatie. Plus la taille d'échantillon augmente plus la loi de Student ressemble à la loi normale. Les deux lois se superposent à partir du moment où le nombre d'échantillons atteint 30 valeurs.
Lorsque nous utiliserons la loi de Student, le facteur d'élargissement s'appellera “t” au lieu de “k”.
Pour déterminer le facteur d'élargissement à appliquer il faut non seulement tenir compte du niveau de confiance souhaité, mais également du nombre de degrés de liberté.
Rappel : Le nombre de degrés de liberté est égal à n-1
La loi de Student est applicable dans tous les cas de figure. La loi normale elle est applicable uniquement lorsque l'on sait que les mesures suivent une loi normale ou que la taille d'échantillon est supérieure à 30.
Evaluation simplifiée de l'incertitude du processus de mesure
Il n'est pas toujours possible d'estimer la certitude de mesures selon les méthodes GUM et 5725. En effet, déterminer les incertitudes de mesure avec autant de finesse peut s'avérer coûteux pour les entreprises.
Ainsi pour les mesures qui ne sont pas critiques pour l'entreprise, il est possible d'utiliser une méthode simplifiée d'évaluation de l'incertitude de mesure.
On émet l'hypothèse que dans le processus de mesure, il existe principalement deux sources d'incertitude. Celles dues :
- à l'instrument utilisé (Moyen)
- aux autres sources d'incertitudes selon les 4M restant (Milieu, Méthode, Main d&rsquo ;œuvre, Matière)
Evaluation de l'incertitude simplifiés :
U
mesure = U
moyen + U
autres
U
moyen = U
autres
U
mesure= 2 x U
moyen
Si l'on souhaite par exemple un processus de mesures permettant d'obtenir un rapport U/T de 1/6 l'appareil de mesure à retenir devrait avoir une incertitude d'étalonnage inférieur ou égal à 1/12.
En effet, 1/6 = Umoyen/T donc Umoyen=T/12.
Prenons l'exemple d'une Tolérance T = 0.1, l'incertitude maximum de l'appareil sera de 0.1/12=0.0083
Tolérancement
En générale, les spécifications attendues sur un produit sont accompagnées d'une tolérance. Il s'agit de la zone de valeurs acceptable que peut prendre la grandeur.
Notation :
- Vc: Valeur cible
- T: Tolérance
On exprimera la spécification de la façon suivante : Vc ± T/2.
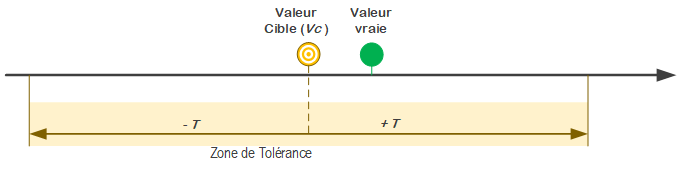
Lien entre tolérance et incertitude
Il est évident que si l'incertitude de mesure est trop élevée au regard de la tolérance, il sera difficile de juger de la conformité des produits.
Considérons les 3 cas suivants :

Le bon sens nous amène à conclure que la situation dans le cas 1 est bien plus favorable que la situation dans le cas 3.
L'adéquation entre l'incertitude U de mesure et la tolérance T est la capabilité.
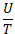
Le rapport entre U et T doit être compris entre 1/2 et 1/10. Cette exigence doit permettre de déterminer le moyen le plus adapté en fonction des besoins et contraintes économiques. En effet, l'acquisition et la maîtrise de certains moyens de contrôle peut s'avérer onéreux.
Gérer la zone de doute
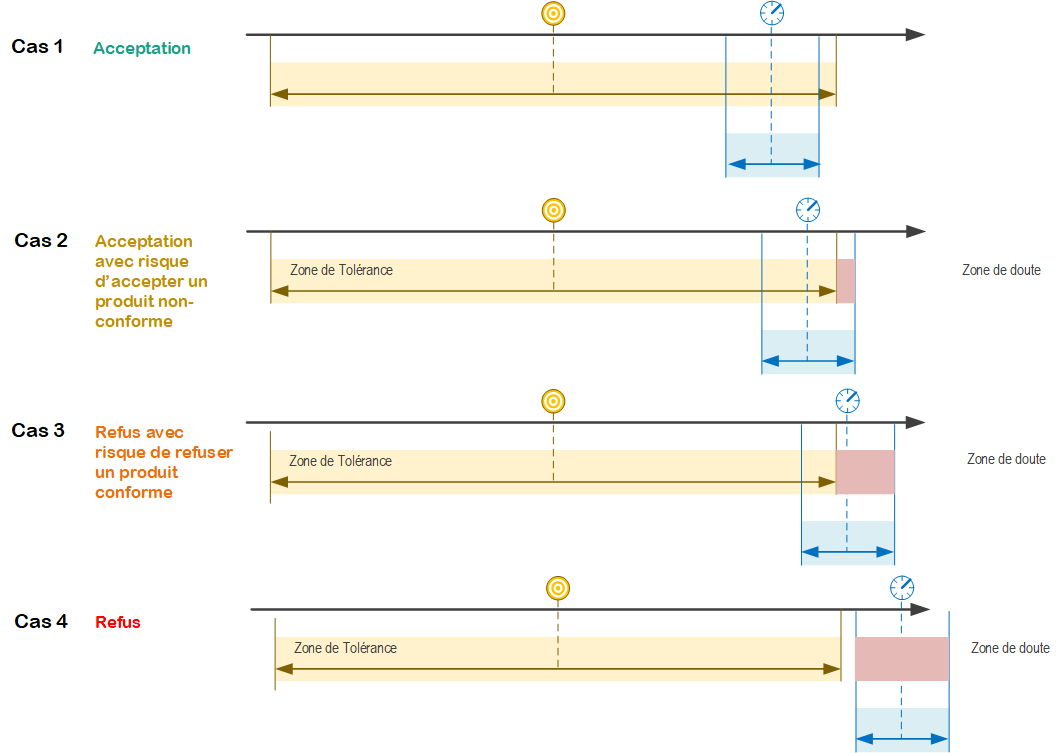
Décider
La définition d'une zone de doute permet de déterminer des règles de décision en fonction de la localisation de la valeur mesurée.

Justesse et fidélité
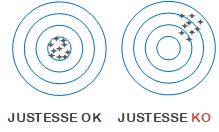
La qualité d'une mesure s'apprécie grâce à son exactitude. L’exactitude représente l'aptitude d'une mesure à donner un résultat proche de la valeur vraie. Celle-ci est composée de deux grandeurs : La justesse et la fidélité. Il est nécessaire de connaître ces deux valeurs si l'on veut comparer des méthodes de mesure, pour s'améliorer ou pour suivre sa stabilité dans le temps.
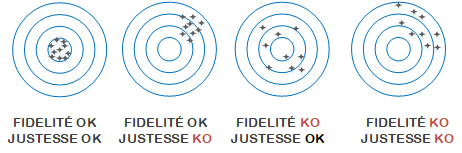
Justesse
NF ISO 5725-1
Pour un instrument de mesure, il s'agira de son aptitude à donner des indications exemptes d’erreurs systématiques.
La justesse permet de savoir si une méthode présente un biais par rapport à une valeur vraie ou une valeur de référence acceptée. Toutefois, cette valeur n'est pas toujours accessible dans la mesure où l'on ne dispose pas forcément de valeur de référence.
Fidélité
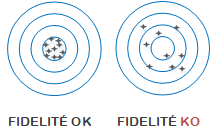
La fidélité et le terme général qui exprime la variabilité entre les mesures. Elle permet de savoir si la forme fournit des résultats comparables lors de répétition pour des conditions de mise en œuvre identiques ou différentes.
La fidélité caractérise la variabilité du processus de mesure. Elle a 2 composantes :
Etude R&R
Il s'agit de l'étude de la variabilité des mesures avec une évaluation de l'impact du moyen de mesure et de l'impact des opérateurs sur le résultat de mesure. Un dossier complet sur l'étude R&R est présent sur le site.
Choisir le processus de mesure
Le choix du processus de mesure est conditionné par :
- la caractéristique à mesurer
- les technologies disponibles pour accéder à ladite caractéristique
- le temps d’obtention du résultat
- le coût d’investissement initial
- le coût de possession du processus
Histoire
Le système international d'unité (SI)
Le Système international d'unités a été créé au moment de la révolution française.
Le Système international d'unités est le système d'unités le plus largement employé au monde ; mais il n'est pas officiellement utilisé aux États-Unis, au Liberia et en Birmanie.
La Conférence générale des poids et mesures décide de son évolution, tous les quatre ans.
Le 13 novembre 2018 : Une réforme majeure du Système international d'unitésa été décidée à Versailles, lors de la 26e Conférence générale des poids et mesures (CGPM), du 13 au 16 novembre. L'ambition de cette grande réforme est d'établir un système d'unités plus cohérent, plus stable et universel. Ainsi le kilogramme, la mole, l’ampère et le kelvin ne reposent plus sur un objet matériel particulier mais sont établi à partir de constantes. (Voir: article : Futurascience du 13.11.18)
Titre : Estimer l'incertitude : mesures, essais
Auteurs : Christophe Perruchet, Marc Priel
Éditeur : FeniXX
ISBN : 2402115270, 9782402115278
Longueur : 150 pages
Définition (Issues de la norme NF X 07-001)
- Grandeur « Attribut d’un phénomène, d’un corps ou d’une substance, qui est susceptible d’être distingué qualitativement et déterminé quantitativement. »
- Valeur d’une grandeur « Expression quantitative d’une grandeur particulière, généralement sous la forme d’une unité de mesure multipliée par un nombre. »
- valeur vraie « Valeur compatible avec la définition d’une grandeur particulière donnée. »
- Mesurage « Ensemble d’opérations ayant pour but de déterminer la valeur d’une grandeur. »
- Mesurande « Grandeur particulière soumise à mesurage. » Le mesurande est ce que l’on souhaite mesurer.
- Grandeurs d’influence « Grandeur qui n’est pas le mesurande mais qui a un effet sur le résultat du mesurage. »
- Justesse « Aptitude d’un instrument de mesure à donner des indications exemptes d’erreurs systématiques. »
- Fidélité (ou répétabilité) « Aptitude d’un instrument de mesure à donner des indications très voisines lors de l’application répétée du même mesurande dans les mêmes conditions de mesurage.
- Exactitude « Aptitude d’un instrument de mesure à donner des indications proches d’une valeur vraie. »
- Incertitude de mesure « Paramètre associé au résultat d’un mesurage, qui caractérise la dispersion des valeurs qui pourraient raisonnablement être attribuées au mesurande. »
- Incertitude-type « Incertitude du résultat d’un mesurage exprimée sous la forme d’un écart-type. »
- L’incertitude-type composée, c’est-à-dire l’incertitude globale associée au résultat d’un mesurage, se calcule alors en faisant la somme des incertitudes-types.
- Étalonnage « Ensemble des opérations établissant, dans des conditions spécifiées, la relation entre les valeurs de la grandeur indiquées par un appareil de mesure, et les valeurs correspondantes de la grandeur réalisées par des étalons. »
- Vérification « Confirmation par examen et établissement de preuves que les exigences spécifiées ont été satisfaites. Le résultat d’une vérification se traduit par une décision de remise en service, d’ajustage, de réparation, de déclassement ou de réforme. »
- Erreur maximale tolérée « Valeurs extrêmes d’une erreur tolérée par les spécifications, les règlements, etc., pour un instrument de mesure donné. »
- Ajustage « Opération destinée à amener un instrument de mesure à un état de fonctionnement convenant à son utilisation. »
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT


